montrer que ∀n∊N la somme de k=0 jusqu'a k=n de K² est egale a n(n+1)(2n+1)/6 puis en deduire la somme de k=0 jusqu'a k=n de K^3
pour la premiere question je m'en sort mais pour la 2eme je suis pas si sur
Somme d'une suite
4 messages
- Page 1 sur 1
Re: somme d'une suite
Bonjour à toi aussi...
En tout cas, c'est sûr que si tu ne nous écris pas ce que tu as tenté, on ne risque pas de pouvoir te dire si c'est bon ou pas...
haithem6 a écrit:montrer que ∀n∊N la somme de k=0 jusqu'a k=n de K² est egale a n(n+1)(2n+1)/6 puis en deduire la somme de k=0 jusqu'a k=n de K^3
pour la premiere question je m'en sort mais pour la 2eme je suis pas si sur
En tout cas, c'est sûr que si tu ne nous écris pas ce que tu as tenté, on ne risque pas de pouvoir te dire si c'est bon ou pas...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: somme d'une suite
Salut,
Pour calculer les sommes\!=\!\sum_{k=1}^nk^\alpha) avec
avec  connu il y a des tonnes de méthodes.
connu il y a des tonnes de méthodes.
Ici, vu le "en déduire" semblant indiquer qu'on doit déduire la valeur de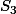 de celle de
de celle de  (et sans doute de celle de
(et sans doute de celle de  bien connue et de celle de
bien connue et de celle de 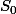 triviale) c'est peut-être ça qui est attendu :
triviale) c'est peut-être ça qui est attendu :
^4<br />=\sum_{k=1}^{n}(k^4\!+\!4k^3\!+\!6k^2\!+\!4k\!+\!1)<br />=\Big(\!\sum_{k=1}^{n}k^4\!\Big)+\!4S_3(n)\!+\!6S_2(n)\!+\!4S_1(n)\!+\!S_0(n))
\!+\!6S_2(n)\!+\!4S_1(n)\!+\!S_0(n)=\Big(\!\sum_{k=2}^{n+1}k^4\!\Big)\!-\!\Big(\!\sum_{k=1}^{n}k^4\!\Big)=(n\!+\!1)^4\!-1)
Qui permet effectivement de trouver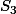 si on connaît
si on connaît  ,
,  et
et 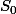 .
.
Bien sûr, le même calcul montre que, pour tout , on a
, on a
=(n\!+\!1)^{\alpha+1}\!-1) où les
où les  sont les coeff. binomiaux.
sont les coeff. binomiaux.
qui permet de calculer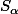 en fonction de
en fonction de 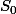 ,
,  ,
,  , . . . ,
, . . . ,  .
.
Pour calculer les sommes
Ici, vu le "en déduire" semblant indiquer qu'on doit déduire la valeur de
Qui permet effectivement de trouver
Bien sûr, le même calcul montre que, pour tout
qui permet de calculer
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
