Somme d'une série entière

[Terminator091]

Quelqu'un aurait une idée pour calculer cette somme ?

[GaBuZoMeu]

Bonjour,
Ça me semble être la partie paire (relativement à ) d'une série assez simple à sommer.
Auitrement dit, il peut être avantageux d'introduire la série soeur avec des sinus hyperboliques.

[tournesol]

Déjà parceque le rayon de convergence de la série "fratrie"() est différent de celui des frère et soeur(inf(, )avec variante lorsque théta est nul).
On a donc le rappel de ce résultat: r(S1+S2)inf(r(S1),r(S2))

[catamat]

Bonjour

Je me demande quelle est (ou doit être) la condition sur x, car si x est négatif :
appelons k le dernier indice, si k pair la somme se comporte comme x^k quand x tend vers -inf, sa limite est donc +inf, par contre si k est impair sa limite toujours en -inf est -inf, cela me semble impossible d'avoir une limite quand k tend vers +inf.

Par contre pour x positif il n'y a pas ce problème.

[GaBuZoMeu]

On somme , et on en prend la partie paire en :
.
Quant au rayon de convergence de la série, vu que est équivalent à quand 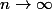(pour ), il est égal à , ce qui est bien normal quand on regarde la somme.

[catamat]

Ok merci j'avais fait ce calcul mais je trouvais



donc le rayon de convergence est assez réduit, là je n'avais pas le bon.

[GaBuZoMeu]

Mais c'est la même chose, catamat !

[tournesol]

Je dirais même plus:

[catamat]

En effet GaBuZoMeu, mais je ne disais pas que c'était différent c'était le rayon qui me posait problème .