Somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 03 Oct 2006, 18:46
par bitonio » 03 Oct 2006, 18:46
Bonjour à tous,
je bloque sur une somme pourtant pas bien compliqué à mon avis ... si vous avez des idées, je suis prenneur :++:
Montrer que
 cos(k \theta) = 2^n cos ( \frac {n \theta } { 2 }) cos ( \frac { \theta } { 2 } )^n)
merci d'avance!
Ciao
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 03 Oct 2006, 18:50
par abcd22 » 03 Oct 2006, 18:50
Bonsoir,
Il suffit de remarquer que la somme est la partie réelle de
^n)
.
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 03 Oct 2006, 19:43
par bitonio » 03 Oct 2006, 19:43
En effet .... euh peux tu me donner une piste je vois pas comment continuer ... merci d'avance!
-
xon
- Membre Relatif
- Messages: 100
- Enregistré le: 24 Aoû 2006, 14:57
-
 par xon » 03 Oct 2006, 20:10
par xon » 03 Oct 2006, 20:10
Salut,
je pense que tu peux calculer
^n)
en mettant en facteur
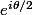
histoire de faire apparaitre un cosinus et tu prends la partie réelle et tu dois plus être loin du compte
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:17
par Zebulon » 03 Oct 2006, 20:17
Bonsoir, pour le membre de gauche :
^n=\sum_{k=0}^n{n\choose{k}}e^{ki{\theta}}<br />\\=\sum_{k=0}^n{n\choose{k}}[{cos(k\theta)+isin(k\theta)}])
dont la partie réelle est
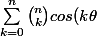)
.
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 03 Oct 2006, 21:09
par bitonio » 03 Oct 2006, 21:09
Au risque de paraitre legerement bete, je ne vois toujours pas comment m'en sortir ... :triste:
J'aimerai juste une piste, pas la solution... merci d'avance
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 03 Oct 2006, 21:11
par bitonio » 03 Oct 2006, 21:11
ah non en fait je crois c'est bon ! j'avais pas vu la formule de trigo :marteau:
merci bcp !!
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 04 Oct 2006, 07:17
par Nicolas_75 » 04 Oct 2006, 07:17
Bonjour,
Une récurrence est également possible, à condition de considérer de front :
\; :\;\left\{\begin{array}{rcl}<br />\displaystyle\sum_{k=0}^n{n\choose k}\cos k\theta&=&\displaystyle 2^n\cos\frac{n\theta}{2}\cos^n\frac{\theta}{2}\\<br />\displaystyle\sum_{k=0}^n{n\choose k}\sin k\theta&=&\displaystyle 2^n\sin\frac{n\theta}{2}\cos^n\frac{\theta}{2}\\<br />\end{array}\right.)
Montrons la première partie de l'hérédité, celle relative à la première formule.
\theta\\<br />=&\displaystyle 1+\sum_{k=1}^n{n\choose k-1}\cos k\theta+\sum_{k=1}^n{n\choose k}\cos k\theta+\cos(n+1)\theta\\<br />=&\displaystyle \sum_{k=1}^{\fbox{n+1}}{n\choose k-1}\cos k\theta+\sum_{k=\fbox{0}}^n{n\choose k}\cos k\theta\\<br />=&\displaystyle \sum_{k=0}^{n}{n\choose k}\cos (k+1)\theta+\sum_{k=0}^n{n\choose k}\cos k\theta\\<br />=&\displaystyle \sum_{k=0}^{n}{n\choose k}\left[\cos(k+1)\theta+\cos k\theta\right]\\<br />=&\displaystyle \sum_{k=0}^{n}{n\choose k}2\cos\left(k+\frac{1}{2}\right)\theta\cos\frac{\theta}{2}\\<br />=&\displaystyle \sum_{k=0}^{n}{n\choose k}2\left(\cos k\theta\cos\frac{\theta}{2}-\sin k\theta\sin\frac{\theta}{2}\right)\cos\frac{\theta}{2}\\<br />=&\displaystyle 2\cos\frac{\theta}{2}\cos\frac{\theta}{2}\sum_{k=0}^n{n\choose k}\cos k\theta-2\cos\frac{\theta}{2}\sin\frac{\theta}{2}\sum_{k=0}^n{n\choose k}\sin k\theta\\<br />=&\displaystyle 2\cos\frac{\theta}{2}\cos\frac{\theta}{2}2^n\cos\frac{n\theta}{2}\cos^n\frac{\theta}{2}-2\cos\frac{\theta}{2}\sin\frac{\theta}{2}2^n\sin\frac{n\theta}{2}\cos^n\frac{\theta}{2}\\<br />=&\displaystyle 2^{n+1}\left(\cos\frac{\theta}{2}\cos\frac{n\theta}{2}-\sin\frac{\theta}{2}\sin\frac{n\theta}{2}\right)\cos^{n+1}\frac{\theta}{2}\\<br />=&\displaystyle 2^{n+1}\cos\frac{(n+1)\theta}{2}\cos^{n+1}\frac{\theta}{2}\\<br />\end{array})
La seconde partie de l'hérédité (avec les sinus) se montre de manière similaire.
Sauf erreur.
Nicolas
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités