Somme de Riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 12 Aoû 2008, 21:45
par MacManus » 12 Aoû 2008, 21:45
Bonsoir !
Est-ce possible d'avoir un peu d'aide pour l'exercice suivant ?
Soit une suite définie par le terme général (pour n
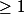
) :
}{(n!)^2} \right )^{\frac{1}{n}})
Je dois écrire
)
comme une somme de Riemann.
Après quelques simplifications, je tombe sur l'expression
 = \frac{1}{n} \left [ \sum_{k=1}^n ln(k^2 + n^2) - 2ln(n!) \right ])
Seulement la soustraction me gène et je ne sais pas finalement s'il s'agit bien d'une somme de Riemann (si mon calcul est correct...)
Merci pour vos précisions !
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 12 Aoû 2008, 21:52
par MacManus » 12 Aoû 2008, 21:52
...peut-être dois-je continuer ma simplification, par exemple en écrivant ln(n!) comme une somme non ?? :arf2:
-
Weensie
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Juil 2008, 18:50
-
 par Weensie » 12 Aoû 2008, 22:19
par Weensie » 12 Aoû 2008, 22:19
tu peux toujours essayer
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 12 Aoû 2008, 22:26
par miikou » 12 Aoû 2008, 22:26
oui c'est bien cela, par contre attention pour la somme de riemann car tu vas avoir qq chose du genre 1/n * somme ln (1+(k/n)²)
-
Weensie
- Membre Naturel
- Messages: 97
- Enregistré le: 14 Juil 2008, 18:50
-
 par Weensie » 12 Aoû 2008, 22:43
par Weensie » 12 Aoû 2008, 22:43
oui on le sent venir !!
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 12 Aoû 2008, 22:46
par MacManus » 12 Aoû 2008, 22:46
eh bien merci Miikou et Weensie !
effectivement Miikou je retrouve ton résultat.
Bonne soirée !
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 12 Aoû 2008, 23:03
par miikou » 12 Aoû 2008, 23:03
jvoulais dire par la que la fonction a integrer sur [0,1] est ln(1+x²), enfin c'etait peut etre evident mais il aurait ete un peu dommage de prendre ln(1+x)
bonne soirée a toi également
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 26 Aoû 2008, 09:54
par jeje56 » 26 Aoû 2008, 09:54
Bonjour à tous !
Je reviens de vacs et j'essaye de me remettre un petit peu aux maths...
Comment écrire ln(n!) sous forme de somme ? Et pourquoi ?
Merci bcp de votre aide ;-)
-
jameso
- Membre Naturel
- Messages: 62
- Enregistré le: 11 Aoû 2006, 15:12
-
 par jameso » 26 Aoû 2008, 10:21
par jameso » 26 Aoû 2008, 10:21
utilise la définition de la factorielles de n et l'identité ln(ab)=ln(a) + ln(b)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
