Somme Riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
guermain
- Messages: 8
- Enregistré le: 29 Déc 2011, 14:40
-
 par guermain » 29 Déc 2011, 15:43
par guermain » 29 Déc 2011, 15:43
Bonjour,
Je cherche une solution pour les deux sommes arithmétiques suivantes :
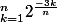
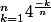
Un grand merci d'avance.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 29 Déc 2011, 16:41
par XENSECP » 29 Déc 2011, 16:41
Bon maintenant que c'est dans le "Supérieur", on peut discuter...
k}{n})})
ça te dis des trucs ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Déc 2011, 16:56
par girdav » 29 Déc 2011, 16:56
Pas besoin de sommes de Riemann, ce sont des sommes calculables.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 29 Déc 2011, 16:56
par XENSECP » 29 Déc 2011, 16:56
girdav a écrit:Pas besoin de sommes de Riemann, ce sont des sommes calculables.
Ok si tu le dis

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Déc 2011, 17:23
par Nightmare » 29 Déc 2011, 17:23
XENSECP a écrit:Bon maintenant que c'est dans le "Supérieur", on peut discuter...
k}{n})})
ça te dis des trucs ?
Comment tu vas t'en sortir avec ça? Il manque le (b-a)/n en facteur.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 29 Déc 2011, 17:29
par XENSECP » 29 Déc 2011, 17:29
Nightmare a écrit:Comment tu vas t'en sortir avec ça? Il manque le (b-a)/n en facteur.
Oh ça va si vous êtes tous contre moi proposez des choses... Moi je pense que c'est Riemann mais bon la prépa c'est loin
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Déc 2011, 17:32
par Nightmare » 29 Déc 2011, 17:32
Ouai mais le truc que tu as écrit c'est pas du Riemann, il manque un facteur qu'est justement pas présent dans l'énoncé. Alors à moins de le faire apparaître, je vois pas comment on s'en sortirait avec Riemann (je dis pas que c'est impossible).
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Déc 2011, 17:56
par girdav » 29 Déc 2011, 17:56
XENSECP a écrit:Oh ça va si vous êtes tous contre moi proposez des choses...
Pour
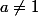
^{n+1}-1}{a-1}-1=\frac{a\cdot a^{\frac 1n}-1-(a-1)}{a-1}=\frac a{a-1}(a^{\frac 1n}-1))
.
-
guermain
- Messages: 8
- Enregistré le: 29 Déc 2011, 14:40
-
 par guermain » 04 Jan 2012, 23:43
par guermain » 04 Jan 2012, 23:43
girdav a écrit:Pour
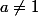
^{n+1}-1}{a-1}-1=\frac{a\cdot a^{\frac 1n}-1-(a-1)}{a-1}=\frac a{a-1}(a^{\frac 1n}-1))
.
Au fait, je ne comprends pas ce passage:
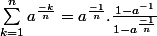
Pourriez-vous m'aider à le démontrer, svp?
Un grand merci d'avance.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 04 Jan 2012, 23:58
par girdav » 04 Jan 2012, 23:58
Tu applique la formule que tu connais pour
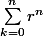
au bon

,

étant fixé.
-
mathelot
 par mathelot » 05 Jan 2012, 07:07
par mathelot » 05 Jan 2012, 07:07
bah vi, ce sont des sommes de progression géométrique :we: Pas de Riemann là dedans.
-
guermain
- Messages: 8
- Enregistré le: 29 Déc 2011, 14:40
-
 par guermain » 09 Jan 2012, 14:20
par guermain » 09 Jan 2012, 14:20
girdav a écrit:Tu applique la formule que tu connais pour
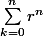
au bon

,

étant fixé.
et tu l'appliques comment dans ce cas?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités