Somme partielle de l'exponentielle

[yos]

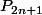
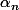
a une racine réelle unique.
Que dire de la suite ?
La décroissance est pas trop dure.
Je trouve diverse minorations pas terribles.
Encore pire pour les majorations.
Pas d'équivalent.

[XENSECP]

Lol comme la somme infinie c'est l'exponentielle, et que l'exp admet "une racine" en "- oo", je dirais que la suite est juste décroissante vers - oo ;)

[yos]

oui c'est .
Peut-on le trouver sans utiliser exp?
J'ai
et aussi

[ThSQ]

avec on a

Ca permet de minorer brutalement par -n.
On peut peut-être majorer par -n/ln(n) mais là c'est dodo time.

[mathelot]

Bj,

est solution de



en résolvant , par la méthode de la variation de la constante



d'où



je n'ai pas réussi à obtenir un équivalent.

[yos]

Merci pour ces idées que je vais explorer.