Bonjour,
comme l'indique l'intitulé du sujet, je cherche une démonstration. Si X suit une loi binomiale de parametres n,p et si Y en est une aussi mais de parametres m,p et si Y et X sont indépendants alors X+Y est une loi binomiale de parametres n+m,p.
Est ce quelqu'un pourrait m'aider?
Somme de loi bionmiales
6 messages
- Page 1 sur 1
en fait je cherche cette demonstration dans le cadre de la lecon sur "schéma de Bernoulli et loi binomiale" et je ne dispose que de l'expression de la proba d'une v.a suivant une loi de binomiale. Je crois savoir qu'on doit utiliser la formule de van der monde mais je n'en sais pas plus.
Est ce que quelqu'un saurait m'aider?
merci
Est ce que quelqu'un saurait m'aider?
merci
X binomiale de paramètres n,p 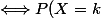=\begin{pmatrix}k\\n\end{pmatrix}p^k(1-p)^{n-k})
Y binomiale de paramètres m,p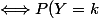=\begin{pmatrix}k\\m\end{pmatrix}p^k(1-p)^{m-k})
X+Y binomiale de paramètres m+n,p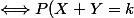=\begin{pmatrix}k\\m+n\end{pmatrix}p^k(1-p)^{m+n-k})
Or
P(X+Y=k)=P(X=0 et Y=k)+P(X=1 et Y=k-1) + .... + P(X=k et Y=0)
P(X+Y=k)=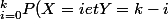)
Si X et Y sont indépendants:
P(X=i et Y=k-i)=P(X=i)P(Y=k-i) (définition de l'indépendance)
Donc dans ce cas
P(X+Y=k)=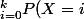P(Y=k-i))
De sorte qu'en remplaçant P(X=i) par sa valeur (ligne 1) et P(Y=k-i) par sa valeur (ligne 2)
Pour démontrer que X+Y est binomiale il suffit d'établir que
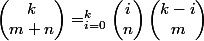
Or ceci est une formule combinatoire qu'on établit en disant que les parties à k éléments de la réunion de deux ensembles disjoints à n et m éléments respectivement, s'obtiennent en combinant toutes les parties à i éléments du premier avec les parties à k-i du second de toutes les façons possibles i allant de 0 à k.
Y binomiale de paramètres m,p
X+Y binomiale de paramètres m+n,p
Or
P(X+Y=k)=P(X=0 et Y=k)+P(X=1 et Y=k-1) + .... + P(X=k et Y=0)
P(X+Y=k)=
Si X et Y sont indépendants:
P(X=i et Y=k-i)=P(X=i)P(Y=k-i) (définition de l'indépendance)
Donc dans ce cas
P(X+Y=k)=
De sorte qu'en remplaçant P(X=i) par sa valeur (ligne 1) et P(Y=k-i) par sa valeur (ligne 2)
Pour démontrer que X+Y est binomiale il suffit d'établir que
Or ceci est une formule combinatoire qu'on établit en disant que les parties à k éléments de la réunion de deux ensembles disjoints à n et m éléments respectivement, s'obtiennent en combinant toutes les parties à i éléments du premier avec les parties à k-i du second de toutes les façons possibles i allant de 0 à k.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
