Somme des séries n^2, n^3 ...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 17 Juin 2006, 00:53
par Sdec25 » 17 Juin 2006, 00:53
Bonjour
J'aimerais savoir comment trouver une formule pour la somme des séries

Maxima peut me calculer cette série, et je peux démontrer les formules par récurrence mais je me demande comment on fait pour les trouver, quelle règle utiliser.
Je sais démontrer la formule pour S = 1 + 2 + 3 + 4 + ... mais pour les puissances de 2 et plus je ne sais pas.
Merci d'avance.
-
Amine.MASS
- Membre Naturel
- Messages: 65
- Enregistré le: 26 Avr 2006, 19:07
-
 par Amine.MASS » 17 Juin 2006, 01:36
par Amine.MASS » 17 Juin 2006, 01:36
salut,
je pense avoir une methode qui n'est pas tres pratique si la puissance de k augumente:
en effet,cherchant

si on arrive à trouver un polynome P de degrés i+1 tq
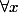
p(x+1)-P(x)=
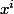
on aurra alors
-P(k)=P(n)-P(1))
pour trouver le polynome pose

en remplaçant tu trouvras i+1 équation tu en déduiras les

et voila tu as la somme voulu
je te propose d'utiliser cette methode pour

pour vérifier:
tu trouveras que P=

donc

=P(n)-P(1)
en simplifiant on obtient la formule conue
(2n+1)}{6})
je voudrais bien savoir s'il y a une methode plus simple
merci.
Cordialement,Amine
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 17 Juin 2006, 09:08
par yos » 17 Juin 2006, 09:08
Plus simple non. Il y a une formule générale pour la somme des
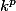
qui fait intervenir les nombres de Bernoulli, mais c'est assez lourd à obtenir.
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 17 Juin 2006, 09:33
par Chimomo » 17 Juin 2006, 09:33
Ceci dit la méthode avec les polynôme permet en effet de trouver des formules pour tous les exposants entiers positifs (et c'est ainsi je crois que les formules ont été trouvées au début).
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 17 Juin 2006, 14:00
par Sdec25 » 17 Juin 2006, 14:00
Merci beaucoup pour votre aide, je trouve cette méthode bien pratique, et pas très compliquée :happy2:
Je viens en effet de redémontrer la formule pour

On peut même utiliser 2 fonctions :
On peut soit s'arranger pour que
-P(n) = x^2$$)
, alors
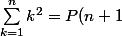 - P(1)$$)
Ou bien pour que
-P(n-1) = x^2 $$)
, dans ce cas
 = \frac {x^3} 3 + \frac{x^2} 2 + \frac x 6)
, et on trouve
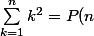 -P(0) = P(n) = \frac {n^3} 3 + \frac{n^2} 2 + \frac n 6 = \frac {n(n+1)(2n+1)} 6$$)
Merci encore
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
