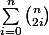Somme des combinaisons

[Houda.9rayti]

Bonsoir tout le monde,

J'ai un devoir à rendre, avec ce qui me semble une erreur dans l'énoncé d'un exercice. On me demande de calculer
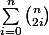
Dès que i dépasse la partie entière de n/2 les combinaisons n'ont plus de sens, ce que je raconte est correct ?
Merci beaucoup

[zygomatique]

salut

déjà il me semble que n est en haut ...

[Houda.9rayti]

Vous avez raison. C'est rectifié maintenant...

[Houda.9rayti]

quelqu'un a une idée comment faire face à cet ambiguïté ?

[Pseuda]

Bonsoir tout le monde,

J'ai un devoir à rendre, avec ce qui me semble une erreur dans l'énoncé d'un exercice. On me demande de calculer
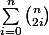
Dès que i dépasse la partie entière de n/2 les combinaisons n'ont plus de sens, ce que je raconte est correct ?
Merci beaucoup

Bonsoir,

Oui il faut s'arrêter avant. Par exemple si n=7, i doit s'arrêter à 3.

Donc à mon sens c'est mal écrit. Il faudrait que sous le signe sigma, il y ait écrit : en plus de i=0.

De mémoire, ce problème se résout en développant et par la formule du binôme.

[Houda.9rayti]

oui c'est bien comme ça qu'on résout ce problème
Que dois-je écrire dans ma copie à votre avis? Signaler l'erreur et ajouter la condition 2i<=n puis résoudre l'exercice?

[Pseuda]

Bonjour,

Oui. Cette condition peut se résumer en . Cela n'empêche pas de résoudre ce problème.

[lionel52]

Bonjour par convention k parmi n = 0 lorsque k > n

[zygomatique]

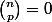
il n'est pas nécessaire de rajouter la condition car par convention lorsque p > n

et effectivement on veut les coefficients binomiaux correspondants aux puissances pairs dans le développement de

il suffit donc de prendre x = 1 et x = -1 ...

[Ben314]

Salut,
On peut éventuellement raisonner différemment : un élément du triangle de pascal, c'est la somme des deux "au dessus" donc si on fait la somme d'une ligne en en prenant un sur 2, ça fait la somme complète de la ligne juste au dessus.
C'est un peu plus court, mais c'est moins "conventionnel" comme méthode.