Somme des chiffres de 7777777^7777777

[buzard]

L'entier N est sans doute équiréparti. effet, la somme
de chiffres de N vaut 241 145 716. Divisée par son nombre exact de chiffres,
ça donne 4,499..


question:

sait-on résoudre les systèmes 3x3 avec des congruences différentes
style

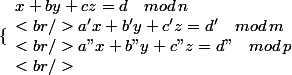
ça ressemble à une extension du lemme chinois (ou théorème des restes chinois si on préfère), mais je ne comprend pas pourquoi tu sépare en trois variable

toujours est-il que la resolution d'un tel système va mener à une infinité de solution, comment fait on pour discriminer la bonne?

[buzard]

pour ce qui veulent faire des stats voila la répartition des chiffres (de 0 à 9):

{5362033, 5359819, 5361837, 5359306, 5361132, 5358380, 5359558, 5356278, 5358172, 5359023}

et la p valeur du du test du chi² pour l'hypothèse nulle d'une répartition uniforme est d'environ 19%. effectivement on a quelques irrégularité par rapport à une répartition uniforme, mais on en est proche loi des grand nombre oblige)

Par contre on remarque "nettement" la tendance exprimer par nodjim sur la surpopulation des chiffres < 5. la p valeur du test d'adequation de Kolmogorov Smirnov n'est que de 8%.

Mais bizarrerie, visuellement j'aurai tendance à dire que les chiffres paires sont moins représenté que les chiffres impaire, mais la p valeur du test ks est de 35%.

le test de wilcoxon donnant respectivement les p valeurs 1% et 15%