Somme de cosinus avec nombre complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Killiotrope
- Messages: 3
- Enregistré le: 07 Oct 2021, 19:07
-
 par Killiotrope » 07 Oct 2021, 23:31
par Killiotrope » 07 Oct 2021, 23:31
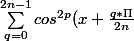}=\frac{2n\frac{2p!}{p!(2p-p)!}}{2^{2p}})
Bonjour, voici un exo sur lequel je bloque. J'ai commencé par appliquer la formule d'Euler et le binôme de Newton, ainsi j'ai le dénominateur que je cherche mais après je ne sais pas quoi faire pour obtenir p parmi 2p.
Pouvez vous m'aider ?
Merci d'avance !
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 08 Oct 2021, 06:49
par Pisigma » 08 Oct 2021, 06:49
Bonjour,
petit problème dans le second membre (2p-p)!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Oct 2021, 16:44
par Ben314 » 08 Oct 2021, 16:44
Salut,
Ton résultat est faux en général : il manque une hypothèse cruciale pour que ça marche, à savoir que p<2n.
Par contre, avec cette hypothèse supplémentaire, c'est relativement simple. On peut effectivement commencer par utiliser la formule d'Euler puis le binôme de Newton pour développer la somme à la puissance 2p ce qui donne une double somme. Ensuite tu fait ce qui est plus que classique, à savoir que tu interverti l'ordre des deux sommations et tu sort de la somme la plus interne tout ce qui ne dépend pas du paramètre de sommation.
Tu doit te retrouver avec la somme la plus interne qui est simplement la somme des termes d'une suite géométrique ce qui permet de calculer sa valeur . . .
Indication : cette valeur est presque toujours nulle, mais il faut supposer en plus que p<2n pour que ta somme soit constante (i.e. ne dépende pas de x). . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Killiotrope
- Messages: 3
- Enregistré le: 07 Oct 2021, 19:07
-
 par Killiotrope » 08 Oct 2021, 20:24
par Killiotrope » 08 Oct 2021, 20:24
Salut, oui j'ai oublié de préciser une condition, mais sur l'énoncé il est indiqué p<n.
J'ai fais comme tu me l'as indiqué mais je bloque de nouveau

.
*\sum_{k=0}^{2p}{\frac{2p!}{k!(2p-k)!}\frac{\exp(-i2xk)-\exp(-2ixk) }{\exp(i\frac{(p-k)\Pi}{n})-1}})
Pourrais-tu m'aider de nouveau ?
Modifié en dernier par
Killiotrope le 08 Oct 2021, 23:57, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Oct 2021, 23:42
par Ben314 » 08 Oct 2021, 23:42
Après Euler + Newton, tu doit trouver ça :
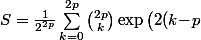ix\big)\sum_{q=0}^{2n-1}\omega^q\ \ \ \text{avec}\ \ \ \omega\!=\!\exp\big(i\frac{(k-p)\pi}{n}\big))
Or, si
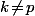
(et que

), alors
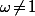
et
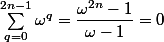
et, si
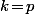
, alors
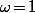
et
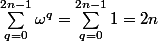
Donc dans la somme
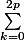
il ne reste que le terme correspondant à
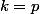
qui est à multiplier par

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Killiotrope
- Messages: 3
- Enregistré le: 07 Oct 2021, 19:07
-
 par Killiotrope » 09 Oct 2021, 00:09
par Killiotrope » 09 Oct 2021, 00:09
J'avais fais une erreur de frappe et j'obtenais bien ce que tu indiques mais je n'avais pas penser a faire les deux cas je trouvais juste la somme des 0 et je ne trouvais pas l'erreur sur le moment.
Merci beaucoup!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités

 .
.