Somme de cos/sin
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
 par Pierre.S » 05 Oct 2014, 15:52
par Pierre.S » 05 Oct 2014, 15:52
Bonjour, je cherche à calculer une somme mais elle est réticente... L'éxercice consiste à trouver une expression de :
=cos(a)+x cos(a+h)+x^2cos(a+2h)+...+x^{n-1}cos(a+(n-1)h))
et
=sin(a)+x sin(a+h)+x^2sin(a+2h)+...+x^{n-1}sin(a+(n-1)h))
Donc j'ai entrepris de calculer
+iS_{n}(x,a,h)=\bigsum_{k=0}^{n-1} x^ke^{i(a+kh)})
Après quelques transformations j'obtiens
^n}{1-xe^{ih}})
Et je n'arrive pas à simplifier cette expression .... Si vous avez des conseils ils sont bienvenu !

-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 05 Oct 2014, 16:00
par deltab » 05 Oct 2014, 16:00
Bonjour.
^n=x^ne^{inh})
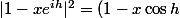^2+x^2\sin^2h=(1-xe^{ih})(\bar{1-xe^{ih}}))
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
 par Pierre.S » 05 Oct 2014, 16:11
par Pierre.S » 05 Oct 2014, 16:11
Merci pour ces éclaircissements mais j'ai déjà essayé de multiplié par le conjugué le dénominateur sans obtenir de résultat alors j'ai peut être pas vu une simplification mais ...
Parce que j'obtiens au dénominateur
+x^2)
mais le numérateur devient tentaculaire...
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 05 Oct 2014, 17:50
par deltab » 05 Oct 2014, 17:50
Pierre.S a écrit:Merci pour ces éclaircissements mais j'ai déjà essayé de multiplié par le conjugué le dénominateur sans obtenir de résultat alors j'ai peut être pas vu une simplification mais ...
Parce que j'obtiens au dénominateur
+x^2)
mais le numérateur devient tentaculaire...
Erreur, mais il est réel. Penses ensuite à séparer partie réelle et partie imaginaire calcul fastidieux mais pas difficile
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
 par Pierre.S » 05 Oct 2014, 20:18
par Pierre.S » 05 Oct 2014, 20:18
deltab a écrit:Erreur
Tu veux dire que j'ai fait une erreur de calcul ?
Et bien en fait je sais que l'on peut s'en sortir avec
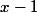
en dénominateur et ça simplifie tout mais je ne sais pas comment y arriver

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Oct 2014, 20:43
par fatal_error » 05 Oct 2014, 20:43
salut,
sinon tu fais ton (gros) bof..
tu prends le numérateur:

avec a facilement identifiable
du coup...
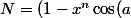) + ix^n\sin(a) = R_N + I_N)
avec
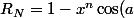)
et
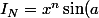)
pareil au dénominateur:
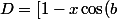 ] + ix\sin(b) = R_D + iI_D)
avec
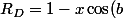)
et
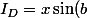)
comme préconisé par deltab, tu multiplies par le dénominateur conjugué idem

au dénominateur

qui est un réel
et au nouveau numérateur
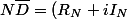(R_D - iI_D))
et on identifie assez facilement
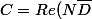 = R_NR_D + I_NI_D\\<br />S = Im(N\bar{D}) = I_NR_D - R_NI_D)
la vie est une fête

-
mathelot
 par mathelot » 05 Oct 2014, 20:51
par mathelot » 05 Oct 2014, 20:51
Pierre.S a écrit: ^{n}-1}{xe^{ih}-1})
bonsoir,
on commence à factoriser les "arcs moitiés"
h}{2})} \, \times \, \frac{x^n e^{i\frac{nh}{2}}-e^{-i\frac{nh}{2}}}{xe^{i\frac{h}{2}}-e^{-i\frac{h}{2}}})
on rend le dénominateur réel en multipliant par la conjuguée
h}{2})} \, \times \, \left( \frac{xe^{-i\frac{h}{2}}-e^{i\frac{h}{2}}}{x^2-2xcos(h)+1} \right) \times \left( x^n e^{i\frac{nh}{2}}-e^{-i\frac{nh}{2}}\right))
on arrange les exponentielles
+1} \, \times \, \left( x^{n+1} e^{i(n-1)h}-x^n \, e^{inh}-x e^{ih}+1\right))
après , il suffit de linéariser (=transformer en somme) et prendre la partie réelle:
-
mathelot
 par mathelot » 05 Oct 2014, 21:09
par mathelot » 05 Oct 2014, 21:09
partie réelle
+1} \, \times \, \left( x^{n+1} cos(a+(n-1)h)- x^n \, cos(a+nh)-x cos(a+h)+cos(a)\right))
partie imaginaire , pareillement
+1} \, \times \, \left( x^{n+1} sin(a+(n-1)h)- x^n \, sin(a+nh)-x sin(a+h)+sin(a)\right))
sauf erreur,
-
mathelot
 par mathelot » 05 Oct 2014, 21:15
par mathelot » 05 Oct 2014, 21:15
Pierre.S a écrit:Merci pour ces éclaircissements explications
.........................c'est pas français , éclaircissements :we: par contre, une somme "réticente" est ..excellent !
-
mathelot
 par mathelot » 05 Oct 2014, 21:20
par mathelot » 05 Oct 2014, 21:20
c'est un néologisme. Au temps pour moi.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 05 Oct 2014, 21:21
par deltab » 05 Oct 2014, 21:21
Bonsoir
Pierre.S a écrit:Merci pour ces éclaircissements mais j'ai déjà essayé de multiplié par le conjugué le dénominateur sans obtenir de résultat alors j'ai peut être pas vu une simplification mais ...
Parce que j'obtiens au dénominateur
+x^2)
mais le numérateur devient tentaculaire...
Désolé! L'erreur de calcul c'est moi qui l'ai faite.
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
 par Pierre.S » 06 Oct 2014, 17:11
par Pierre.S » 06 Oct 2014, 17:11
Pas de soucis !
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
 par Pierre.S » 06 Oct 2014, 17:20
par Pierre.S » 06 Oct 2014, 17:20
Et bien merci à tous je m'attendais a quelque chose de plus élégant mais s'il le faut je m'accommoderai de ça !
Pour ce qui est des expressions farfelues je répondrai que "le mot cristallise la pensée" et j'aime avoir quelques pensées cocasses en plus je trouve ça vraiment récréant de personnifier des expressions ! :ptdr:
Enfin bref sur ceux bonne continuation à ce chaleureux forum ! :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
mais le numérateur devient tentaculaire...
mais le numérateur devient tentaculaire...