Calculer
Somme de combinaisons
3 messages
- Page 1 sur 1
somme de combinaisons
Bonjour à tous, histoire de relancer le forum, voici une petite question à laquelle je n'ai pas encore répondu :
Calculer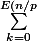}C_{n}^{kp}) , où
, où  est un entier inférieur à
est un entier inférieur à  et
et ) est la partie entière de
est la partie entière de 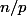 .
.
Calculer
Bonjour,
je suggere de calculer (1+x)^n, avec x une racine pieme de l'unite, et de faire des combinaisons lineaires a coefficients complexes de ces expressions pour eliminer les coefficients binomiaux qui ne t'interessent pas. Par exemple pour calculer la somme sur k des coeff. binomiaux C(n,2k), on additionne (1+1)^n et (1+(-1))^ n, 1 et -1 etant des racines secondes de l'unite. Tu peux commencer avec p=3 pour voir comment ca marche. Ensuite on fait apparaitre des sinus et cosinus en utilisant 1+x=x^(1/2) (x^(-1/2)+x^(1/2)) et les formules d'Euler.
Bonne journee
je suggere de calculer (1+x)^n, avec x une racine pieme de l'unite, et de faire des combinaisons lineaires a coefficients complexes de ces expressions pour eliminer les coefficients binomiaux qui ne t'interessent pas. Par exemple pour calculer la somme sur k des coeff. binomiaux C(n,2k), on additionne (1+1)^n et (1+(-1))^ n, 1 et -1 etant des racines secondes de l'unite. Tu peux commencer avec p=3 pour voir comment ca marche. Ensuite on fait apparaitre des sinus et cosinus en utilisant 1+x=x^(1/2) (x^(-1/2)+x^(1/2)) et les formules d'Euler.
Bonne journee
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
