Somme de binomiaux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 26 Nov 2022, 19:07
par mathelot » 26 Nov 2022, 19:07
moijesuissansE a écrit:Bonjour,
On me demande de partir de cette expression, dont j'ai donné le résultat
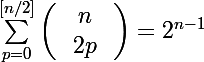
Pour calculer 2p, on traite deux cas: p pair , p=2k et p impair p=2k+1:

-
mathelot
 par mathelot » 26 Nov 2022, 19:20
par mathelot » 26 Nov 2022, 19:20
moijesuissansE a écrit:, je n'arrive pas a déduire cette formule des deux précédentes:
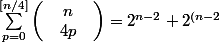/2}cos(\frac{n\pi }{4}))
i)
Développer
^n)
avec la formule du binôme et l'égaliser à la forme trigo
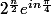
ii)
On égalise les parties réelles, on en déduit :
^n)=\sum_{k=0}^{\left[ \frac{n}{4} \right]} \, \binom{n}{4k}- \sum_{k=0}^{\left[ \frac{n -2}{4} \right]} \, \binom{n}{4k +2}=2^{\frac{n}{2}} cos(n\frac{\pi}{4})) (*)
(*) (**)
(**)iv)
on additionne les égalités (*) et (**), on en déduit le résultat demandé.
-
moijesuissansE
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Mai 2021, 13:32
-
 par moijesuissansE » 27 Nov 2022, 09:26
par moijesuissansE » 27 Nov 2022, 09:26
D'accord je vois merciiiii vraiment, c'est génial
-
moijesuissansE
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Mai 2021, 13:32
-
 par moijesuissansE » 27 Nov 2022, 09:28
par moijesuissansE » 27 Nov 2022, 09:28
Pour ce qui est de cette formule,
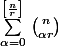
Je me demande ce qu'elle représente pour le triangle de Pascal, concrètement elle représente quoi ?
-
moijesuissansE
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Mai 2021, 13:32
-
 par moijesuissansE » 27 Nov 2022, 15:04
par moijesuissansE » 27 Nov 2022, 15:04
Je trouve en réalité que cela correspond à la partie entière de (2^n)/r
Mais comment cela ce fait-il ?
-
mathelot
 par mathelot » 27 Nov 2022, 19:09
par mathelot » 27 Nov 2022, 19:09
moijesuissansE a écrit:Je trouve en réalité que cela correspond à la partie entière de (2^n)/r
Mais comment cela ce fait-il ?
on a vu la formule:
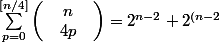/2}cos(\frac{n\pi }{4}))
Quand n est pair,
)
s'annule et on a bien ta formule,
par contre pour n de la forme
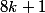
,
=\frac{\sqrt{2}}{2})
et
/2}cos(\frac{n\pi }{4}))
peut être supérieur à 1.
Regardons pour n=9 et r=4:

tandis que
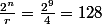
La formule n'est pas vérifiée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités