moijesuissansE a écrit:pour le début normalement non, je suis juste censé rappeler des résultats et en déduire le reste,
mais par la suite on me demande de démontrer une formule générale en faisant intervenir des complexes sous forme exponentielle :
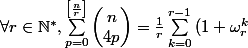^{n}})
avec :
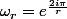
Bonsoir,
après calculs, je trouve:
^n=\sum_{\alpha=0}^{\left[\frac{n}{r} \right]} \, \binom{n}{\alpha r })
Il n'y aurait pas une erreur d'énoncé ?
remarque: j'ai testé avec succès ma formule pour n=10,r=3.
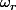
vaut j, (avec
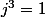
),

, ce qui facilite les calculs.
Pour obtenir la formule demandée:Développer les puissances n-ièmes avec la formule du binôme
Permuter les deux sommations:
on obtient une somme de sommes de progressions géométriques,certaines progressions sont de raison 1,
d'autres de raison différente de 1.
Sommer des progressions géométriques en discutant si
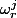
vaut 1 ou non,
ce qui est habituel quand on somme des progressions géomètriques.
