Bonjour tout le monde,j'ai besoin d'un gros coup de pouce pour un exo...
On suppose que chaque individu engendre un nombre d'enfnats suivant une mem loi qu'une variable aléatoire

d'espérance m finie et de fonction génératrice

On note
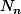
le nombre d'enfants à la n-ieme génération
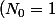)
a)On note
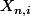
le nombre d'enfnats d'un i-ieme individu de la n-ieme génération.Montrer que
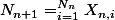
b)On suppose que les var X

avec

des entiers sont indépendantes dans leur ensemble.
Montrer que pour tout

est indépendnat de
_{i\in N})
.En déduire que la fonction génératrice de
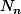
est

.
c)On note
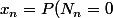)
la probabilité d'extinction de la n-ieme génération.Montrer que
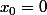
puis que pour tout entier

non nul,
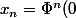)
.En déduire
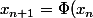)
d)Justifier que

est continue et croissante sur

puis en déduire que la suite
)
converge vers

qui est le plus petit point fixe de

sur

.
alors,
pour a)je vois pas du tout!(une récurrence peut-etre?)
pour b) on sait que les
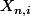
sont indépendnats dans leur ensemble donc
=0)
et pour montrer que
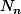
est indépendnat des
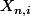
il faut montrer que
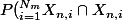=0)
??
pour c)
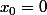
ok
aprés je sais pas trop (encore une récurrence?)
