Sommation, demande explications
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 14:45
par klink60 » 04 Aoû 2008, 14:45
Bonjour,
J'ai cet exercice à résoudre :
Calculer :
)
la solution est :

Je ne comprends pas comment trouver la solution .
j'ai bien vu que
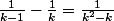
mais comment faut-il faire pour trouver

...
Merci
PS: je ne pense pas que c'est du niveau "supérieur"...
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 04 Aoû 2008, 14:49
par lapras » 04 Aoû 2008, 14:49
salut,
en fait dans ta somme tous les termes s'annule sauf le premier (1) et le dernier (1/n).
-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 14:51
par klink60 » 04 Aoû 2008, 14:51
Oui, mais COMMENT as-tu fait pour trouver la solution ? :cry:
-
john32
- Membre Relatif
- Messages: 239
- Enregistré le: 08 Juil 2008, 10:34
-
 par john32 » 04 Aoû 2008, 14:55
par john32 » 04 Aoû 2008, 14:55
Je comprends pas vraiment le pb si tu arrive a montrer l'égalité entre les deux membres (gauche et droite) pour le terme général de la somme alors c'est bon puisque ta somme commence et finit aux mêmes indices de chaque côté :hum:
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Aoû 2008, 14:56
par Clembou » 04 Aoû 2008, 14:56
klink60 a écrit:Oui, mais COMMENT as-tu fait pour trouver la solution ?

On appelle ça une série téléscopique. Il faut développer ton opérateur

-aires en opérateurs binaires et remarquer que des termes s'annulent deux à deux.
Développer ton opérateur

-aires en opérateurs binaires, c'est faire :

-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Aoû 2008, 14:56
par Clembou » 04 Aoû 2008, 14:56
john32 a écrit:Je comprends pas vraiment le pb si tu arrive a montrer l'égalité entre les deux membres (gauche et droite) pour le terme général de la somme alors c'est bon puisque ta somme commence et finit aux mêmes indices de chaque côté :hum:
Notre ami doit juste s'entraîner à développer des opérateurs n-aires en opérateurs binaires.
-
john32
- Membre Relatif
- Messages: 239
- Enregistré le: 08 Juil 2008, 10:34
-
 par john32 » 04 Aoû 2008, 14:57
par john32 » 04 Aoû 2008, 14:57
Oups boulette mal lu l'énoncé
-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 14:57
par klink60 » 04 Aoû 2008, 14:57
En fait la solution est donnée dans le livre.
-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 14:59
par klink60 » 04 Aoû 2008, 14:59
Explique moi comment faire...
Au risque de paraitre pour un benêt fini...
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Aoû 2008, 15:01
par Clembou » 04 Aoû 2008, 15:01
klink60 a écrit:En fait la solution est donnée dans le livre.
Oui ! Et si j'ai bien compris, tu veux savoir comment ils ont trouvé la solution... Fais ce que je te demande et tu verras que la solution se dévoilera...
Clembou a écrit:On appelle ça une série téléscopique. Il faut développer ton opérateur

-aires en opérateurs binaires et remarquer que des termes s'annulent deux à deux.
Développer ton opérateur

-aires en opérateurs binaires, c'est faire :

-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 15:08
par klink60 » 04 Aoû 2008, 15:08
je me lance :
+(\frac{1}{3-1}-\frac{1}{3})+(\frac{1}{4-1} -\frac{1}{4}))
...
mais je m'arrête à quel moment...
J'ai compris que les termes s'annulaient deux à deux.
Comment savoir ce qu'il me reste à la fin ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Aoû 2008, 15:14
par Clembou » 04 Aoû 2008, 15:14
klink60 a écrit:je me lance :
+(\frac{1}{3-1}-\frac{1}{3})+(\frac{1}{4-1} -\frac{1}{4}))
...
mais je m'arrête à quel moment...
J'ai compris que les termes s'annulaient deux à deux.
Comment savoir ce qu'il me reste à la fin ?
EDIT : Oups, j'avais compris que tu n'avais pas compris pourquoi les termes s'annulaient.
Ce qui te reste à la fin : comme tous les termes deux à deux s'en vont... qu'est ce qui va rester ? Remarque que tu n'as pas barré le tout premier terme. A la fin, tu ne devras pas barré un autre terme, lequel ?
-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 15:18
par klink60 » 04 Aoû 2008, 15:18
oui j'ai vu.
Une fois que tu as remarqué ça quelle est la procédure ?
-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 15:20
par klink60 » 04 Aoû 2008, 15:20
le terme avec n ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Aoû 2008, 15:39
par Clembou » 04 Aoû 2008, 15:39
klink60 a écrit:le terme avec n ?
Voilà tu as tout compris ! Car en fait tu barres tous les termes pour

... Donc il te restera le terme en
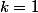
et
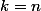
...
-
klink60
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Aoû 2008, 12:44
-
 par klink60 » 04 Aoû 2008, 16:44
par klink60 » 04 Aoû 2008, 16:44
Bien, ça marche, merci
Donc si je me retrouve une fois de pus devant un exercice de ce genre, quelle est la démarche à adopter ?
On doit à chaque fois développer pour essayer de trouver "le truc" ?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Aoû 2008, 16:52
par Clembou » 04 Aoû 2008, 16:52
klink60 a écrit:Bien, ça marche, merci
Donc si je me retrouve une fois de pus devant un exercice de ce genre, quelle est la démarche à adopter ?
On doit à chaque fois développer pour essayer de trouver "le truc" ?
En fait, il faut avoir l'expérience de sentir le truc. Quand tu seras habitué à ce genre de suites (qu'on appelle série), tu verras le truc

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
-aires en opérateurs binaires et remarquer que des termes s'annulent deux à deux.
-aires en opérateurs binaires, c'est faire :
...