Sommation de combinaisons 2
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ihsen
- Membre Naturel
- Messages: 13
- Enregistré le: 29 Juin 2017, 09:42
-
 par Ihsen » 05 Nov 2017, 03:29
par Ihsen » 05 Nov 2017, 03:29
Bonjour à vous tous.
Encore avec des exercices basiques,cette fois on me demande de démontrer les égalités suivantes tels que
pour tout (n,p) appartenant a N² avec p compris entre 0 et n intervalle fermé on a :
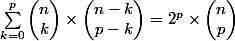
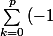^{k}\begin{pmatrix}<br />n\\ <br />k<br />\end{pmatrix}\times \begin{pmatrix}<br />n-k\\ <br />p-k<br />\end{pmatrix}}=0)
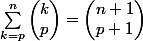
Merci pour votre aide.
-
aviateur
 par aviateur » 05 Nov 2017, 09:07
par aviateur » 05 Nov 2017, 09:07
Bonjour
il y a surement plusieurs façons de faire mais le plus simple:
pour le 1 (et le 2) dans les sommes tu remplaces par les factorielles et tu fait apparaître binomial(n,p).
A toi de faire maintenant.
-
Ihsen
- Membre Naturel
- Messages: 13
- Enregistré le: 29 Juin 2017, 09:42
-
 par Ihsen » 05 Nov 2017, 11:36
par Ihsen » 05 Nov 2017, 11:36
aviateur a écrit:Bonjour
il y a surement plusieurs façons de faire mais le plus simple:
pour le 1 (et le 2) dans les sommes tu remplaces par les factorielles et tu fait apparaître binomial(n,p).
A toi de faire maintenant.
Oui ça a marché pour le 1 et le 2,mais pour le 3 que faire?
-
aviateur
 par aviateur » 05 Nov 2017, 12:17
par aviateur » 05 Nov 2017, 12:17
Rebonjour pour le 3. je n'ai pas regardé de près . Essaye une récurrence sur n.
-
aviateur
 par aviateur » 05 Nov 2017, 12:26
par aviateur » 05 Nov 2017, 12:26
Rebonjour
Une autre possibilités pour le 3. c'est de dire que la somme correspond au nombre de sous-ensembles d'au moins p éléments d'un ensemble à n éléments. Et tu essayes de voir que c'est aussi le nombre de sous-ensemble à p+1 éléments d'un ensemble à n+1 éléments
-
Ihsen
- Membre Naturel
- Messages: 13
- Enregistré le: 29 Juin 2017, 09:42
-
 par Ihsen » 05 Nov 2017, 12:43
par Ihsen » 05 Nov 2017, 12:43
aviateur a écrit:Rebonjour pour le 3. je n'ai pas regardé de près . Essaye une récurrence sur n.
Oui c'était plutôt simple j'aurais du m'en douter.
Merci bcps !

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Nov 2017, 13:30
par chan79 » 05 Nov 2017, 13:30
salut
Pour le dernier, on peut faire une somme téléscopique.
La formule de Pascal donne:
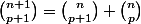
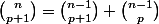
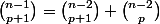
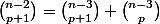
...
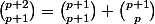
En ajoutant
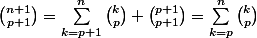
Ci-dessous, le rouge est la somme des verts.
- Fichiers joints
-

- image.gif (9.37 Kio) Vu 266 fois
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités