Solutions périodiques d'une équadiff

par **Nightmare** » 23 Aoû 2010, 13:25

Hello,

Dans le même genre d'idée que ce topic de benekire, je propose l'exercice classique suivant :

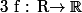
Soit l'équation différentielle y''=y+f où est continue non constante.

Montrer qu'il y a au plus une solution périodique

Pas difficile mais à faire au moins une fois je présume.

:happy3:

par **dibeteriou** » 23 Aoû 2010, 20:48

J'en profite pour poser une question (dont je n'ai pas la réponse) :

On considère une équation différentielle linéaire homogène du type :

où

est 1-périodique. En général,

n'est pas 1-périodique (par contre l'application

est un automorphisme de l'espace des solutions).

Je cherche un contre exemple non trivial.