Bonjour,
Voilà j'ai un exercice sur une équation aux dérivées partielles dont je dois trouver la solution (jamais abordé ce type d'exercice en cours). Je connais la règle de chaîne mais je veux bien un peu d'aide sur la démarche.
https://zupimages.net/viewer.php?id=22/39/1j44.png
1)Calculer les dérivées partielles secondes de g en fonction de celles de f
2)En déduire que f vérifie l'équation une si et slm si g vérifie l'équation suivante :
dg/du = 0
3) Conclure. (Je ne sais pas quoi conclure)
Solution d'une équation aux dérivées partielles.
4 messages
- Page 1 sur 1
Re: Solution d'une équation aux dérivées partielles.
bonsoir lisa,
=g(u;v) ; g(u;v)=f(u;v+u^3))
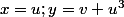
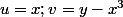
à la question (1)
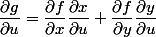
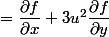
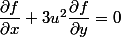
si et seulement si:
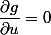
g est donc fonction uniquement de v
il existe donc une fonction telle que
telle que
=\phi(v)=\phi(y-x^3))
L'ensemble des solutions est donc de la forme: \longrightarrow \phi(y-x^3)) où
où  est une fonction dérivable.
est une fonction dérivable.
à la question (1)
si et seulement si:
g est donc fonction uniquement de v
il existe donc une fonction
L'ensemble des solutions est donc de la forme:
Re: Solution d'une équation aux dérivées partielles.
voici mes calculs:
=f(u,v+u^3)=f(x,y))
avec et
et 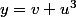
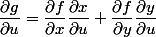
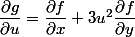
 +6u \dfrac{\partial f}{ \partial y})

remarque; f ne se dérive pas par rapport à u, mais par rapport à x (idem pour v , f se dérive par rapport à y)




avec
remarque; f ne se dérive pas par rapport à u, mais par rapport à x (idem pour v , f se dérive par rapport à y)
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
