Solution particulières EDL d'ordre 2 à coeff constant

par **Viko** » 05 Nov 2017, 14:53

Bonjour,

Je cherche à démontrer qu'une solution particulière de l'EDL d'ordre 2 :

est la fonction

où

est un polynôme de même degrés

et

désigne la multiplicité de

pour le polynôme

j'ai essayé de foncer tête baissé en calculant les dérivées

puis en calculant

mais sa n'a pas l'air d'aboutir :gene:

des idées ?

par **capitaine nuggets** » 05 Nov 2017, 14:58

Salut !

Que sont

et

?
D'après mes souvenirs, une solution particulière est de la forme

, où

est de même degré que

. Exprime alors les coefficients de

en fonction de ceux de

.

par **Viko** » 05 Nov 2017, 15:01

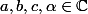
!, je vais essayer ta méthode