Solution particuliere d'une equa diff

[bourbaki]

bonjour tlm
j'ai un petit exo que je n'arrive pas à faire
il s'agit de trouver une solution pariculiere d'une equa diff de la forme:
(x²+1)y"+xy'-4y=0
cette solution particuliere est sous forme polynominale.
je sais qu'il faut determiner le terme dominant du polynome mais je sais pas comment y procéder :cry:

[Nightmare]

Bonjour

On note deg(P) le degré du polynôme recherché

On a alors deg(P'')=deg(P)-2
Ainsi :

de même :

et

de plus

Ainsi deg(P) vérifie :
deg(P)+deg(P)-deg(P)=0
c'est à dire deg(P)=0

Ton polynôme est donc constant

Je te laisse continuer

:happy3:

[bourbaki]

désolé Nightmare car mon polynome n'est pas constant mais du second degré mais je ne sais pas comment arriver a ce résulatat
voila l'enoncé exact et le corrigé
http://www.post-bac.com/j/mod_perl/got.pl?dir=m/mpsi/equadiff/1cfncst/gen/401 :help:

[Nightmare]

Ton polynôme ne peut pas être de degré 2 :

On pose P(x)=ax²+bx+c

On a alors P'(x)=2ax+b
et P''(x)=2a

Ainsi :


On veut que ce polynôme soit nul, donc par identification : -2a=0 soit a=0 ; -3b=0 soit b=0 et -2a+c=0 soit c=0

:happy3:

[bourbaki]

t'as pas jeté un coup d'oeil sur le lein que je t'ai envoyé :hein:
http://www.post-bac.com/j/mod_perl/...1cfncst/gen/401
:zen:

[LN1]

Ton lien ne mène à rien chez moi. Mais Nightmare à tort : dans son développement les termes en x² disparaissent (de plus il s'agit de x² + 1)

pour en revenir à ton problème : regarde le sort du terme de plus haut degré en x, pour
*Dans 4P(x) c'est
*Dans xP'(x) c'est on dérive une fois -->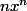, puis on multiplie par x
*Dans x²P"(x), c'est on dérive deux fois --> , puis on multiplie par x²
* dans P"(x), il n'y en a pas car P"(x) est de degré n - 2
*dans (x²+1)P"(x) + xP'(x) - 4 P(x), c'est , c'est à dire


or il faut que le terme en soit nul. Mais est non nul donc il faut que n² - 4 = 0. Ce qui ne se produit que pour n = 2.

le polynôme ne peut donc être que de degré 2

[bourbaki]

ah oui c'est ça . merci bien pour ton aide :id: