Bonjour,
Alors j'ai une équation différentielle : x' - 3x(t) = (3tcarré + 1)(cos(3t)) dont je dois trouver une solution particulière. J'ai pris la forme : (atcarré + b)(cos3t)
Quand je dérive du coup ça fait 2atXcos(3t) - 3sin(3t)(atcarré + b)
Quand j'injecte dans l'équation ça me donne : 2atcos(3t) - 3sin(3t)(atcarré + b) - 3(atcarré + b)cos(3t) =
(3tcarré + 1)cos(3t)
De là, je ne sais pas comment faire pour trouver a et b
Solution particulière d'une équa diff.
12 messages
- Page 1 sur 1
Re: Solution particulière d'une équa diff.
Bonsoir Lisa,
On peut additionner les solutions particulières. On cherche donc d'abord une solution particulière de l'équation)
sous la forme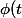=a cos(3t)+b sin(3t))
on trouve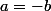 et
et  d'où
d'où  et
et 
Il ne reste plus qu'à trouver une solution particulière de l'équation:
)
On peut additionner les solutions particulières. On cherche donc d'abord une solution particulière de l'équation
sous la forme
on trouve
Il ne reste plus qu'à trouver une solution particulière de l'équation:
Re: Solution particulière d'une équa diff.
mathelot a écrit:Il ne reste plus qu'à trouver une solution particulière de l'équation:(**) ,
En faisant "varier la constante" et en demandant au logiciel Wolfram Alpha de calculer une primitive,
on obtient comme solution particulière de (**) :
explications:
La solution générale de l'équation (**) sans second membre (dite équation homogène) est
On cherche une solution particulière de l'équation (**) avec second membre sous la
forme
On a donc:
et puis on a demandé à Wolfram Alpha de calculer cette primitive (***).
On obtient l'application
Modifié en dernier par mathelot le 13 Fév 2022, 19:53, modifié 2 fois.
Re: Solution particulière d'une équa diff.
mathelot a écrit:
Il ne reste plus qu'à trouver une solution particulière de l'équation:($)
Suite au post précédent, pour revenir à ton exercice, on peut chercher une solution particulière s de ($) sous la forme:
où a,b,c,d,f,g sont des réels à déterminer.
ça donne un système de six égalités à six inconnues que l'on résout aisément (facilement).
On retrouve (on doit retrouver) la solution particulière calculée par Wolfram Alpha.
Re: Solution particulière d'une équa diff.
lisachatroux a écrit:
Alors j'ai une équation différentielle : x' - 3x(t) = (3tcarré + 1)(cos(3t)) dont je dois trouver une solution particulière. J'ai pris la forme : (atcarré + b)(cos3t)
ce qui ne va pas dans la forme de ta solution particulière , c'est qu'il manque la partie avec sin(3t)
destinée à simplifier le sin(3t) issu de la dérivation du cos(3t)
Re: Solution particulière d'une équa diff.
Coucou @mathelot,
Notre prof nous a demandé de ne pas résoudre l'équa diff avec la méthode de variation de la constante du coup j'ai du mal avec l'injection. Je ne comprends pas à partir du moment où tu dis que a = -b et que 6b=1
Pour la partie avec sin(3t), c'est 0sin(3t) donc ça ne change rien non ?
Notre prof nous a demandé de ne pas résoudre l'équa diff avec la méthode de variation de la constante du coup j'ai du mal avec l'injection. Je ne comprends pas à partir du moment où tu dis que a = -b et que 6b=1
Pour la partie avec sin(3t), c'est 0sin(3t) donc ça ne change rien non ?
Re: Solution particulière d'une équa diff.
lisachatroux a écrit:j'ai du mal avec l'injection. Je ne comprends pas à partir du moment où tu dis que a = -b et que 6b=1
Soit l'équation x'-3x=cos(3t) (*) pour tout t réel.
On cherche une solution particulière
On égalise les coefficients.
d'où:
d'où
Modifié en dernier par mathelot le 14 Fév 2022, 19:03, modifié 1 fois.
Re: Solution particulière d'une équa diff.
mathelot a écrit:
Il ne reste plus qu'à trouver une solution particulière de l'équation:($)
Suite au post précédent, pour revenir à ton exercice, on peut chercher une solution particulière s de ($) sous la forme:
où a,b,c,d,f,g sont des réels à déterminer.
ça donne un système de six égalités à six inconnues que l'on résout aisément (facilement).
calcule s'(t) puis -3s(t) puis s'(t)-3s(t)
On a l'application linéaire
en entrée de
et comme image par F, on doit obtenir la fonction
Re: Solution particulière d'une équa diff.
Bonjour,
x' - 3x = (3tcarré + 1)*cos(3t)
Sol particulière de la forme : x = (at²+bt+c)*sin(3t) + (dt²+et+f)*cos(3t)
x' = (3at²+3bt+3c+2dt+e)*cos(3t) + (2at+b-3dt²-3et-3f)*sin(3t)
x'-3x = (3at²+3bt+3c+2dt+e-3dt²-3et-3f)*cos(3t) + (2at+b-3dt²-3et-3f-3at²-3bt-3c)*sin(3t)
A identifier avec x' - 3x = (3t² + 1)*(cos(3t))
--> le système :
2at+b-3dt²-3et-3f-3at²-3bt-3c= 0 pour tout t
3at²+3bt+3c+2dt+e-3dt²-3et-3f = 3t²+1 (pour tout t)
b-3c-3f= 0 (t=0)
-a-2b-3c-3d-3e-3f= 0 (t=1)
-5a+4b-3c-3d+3e-3f= 0 (t=-1)
3a-3d = 3
3c+e-3f = 1
3b+2d-3e=0
Système qui résolu donne : a = 1/2 ; b = 1/3 ; c = 2/9 ; d = -1/2 ; e = 0 ; f = -1/9
Une solution particulière de x' - 3x = (3t² + 1)*cos(3t) est :
x = (1/2.t² + 1/3.t + 2/9)*sin(3t) - (1/2.t² + 1/9)*cos(3t)

x' - 3x = (3tcarré + 1)*cos(3t)
Sol particulière de la forme : x = (at²+bt+c)*sin(3t) + (dt²+et+f)*cos(3t)
x' = (3at²+3bt+3c+2dt+e)*cos(3t) + (2at+b-3dt²-3et-3f)*sin(3t)
x'-3x = (3at²+3bt+3c+2dt+e-3dt²-3et-3f)*cos(3t) + (2at+b-3dt²-3et-3f-3at²-3bt-3c)*sin(3t)
A identifier avec x' - 3x = (3t² + 1)*(cos(3t))
--> le système :
2at+b-3dt²-3et-3f-3at²-3bt-3c= 0 pour tout t
3at²+3bt+3c+2dt+e-3dt²-3et-3f = 3t²+1 (pour tout t)
b-3c-3f= 0 (t=0)
-a-2b-3c-3d-3e-3f= 0 (t=1)
-5a+4b-3c-3d+3e-3f= 0 (t=-1)
3a-3d = 3
3c+e-3f = 1
3b+2d-3e=0
Système qui résolu donne : a = 1/2 ; b = 1/3 ; c = 2/9 ; d = -1/2 ; e = 0 ; f = -1/9
Une solution particulière de x' - 3x = (3t² + 1)*cos(3t) est :
x = (1/2.t² + 1/3.t + 2/9)*sin(3t) - (1/2.t² + 1/9)*cos(3t)
Re: Solution particulière d'une équa diff.
Juste un tout petit mot et je disparais.
Au tout début, quand tu recopies l'énoncé, tu écris l'équation : = (3t^2 + 1)(cos(3t)))
Il faudrait écrire : - 3x(t) = (3t^2 + 1)(cos(3t)))
Ca ne change pas grand chose. Les matheux qui lisent ont compris et ont rectifié. C'était sous-entendu.
Mais quand on n'est pas à l'aise, il faut éviter les sous-entendus. La formule rigoureuse c'est celle que j'ai écrite.
L'écriture avec les sous-entendus, c'est réservé aux experts.
On a le droit d'utiliser des écritures raccourcies, si on est 100% conscient que c'est une écriture raccourcie, et si on est à tout moment capable de remplacer l'écriture raccourcie par l'écriture rigoureuse.
Si on n'est pas conscient que c'est une écriture raccourcie, alors certes, c'est plus rapide à taper, mais c'est source d'erreurs.
Ici, quitte à raccourcir l'écriture, on devrait écrire :(cos(3t))) ... et ça devient illisible, même pour un expert.
... et ça devient illisible, même pour un expert.
Au tout début, quand tu recopies l'énoncé, tu écris l'équation :
Il faudrait écrire :
Ca ne change pas grand chose. Les matheux qui lisent ont compris et ont rectifié. C'était sous-entendu.
Mais quand on n'est pas à l'aise, il faut éviter les sous-entendus. La formule rigoureuse c'est celle que j'ai écrite.
L'écriture avec les sous-entendus, c'est réservé aux experts.
On a le droit d'utiliser des écritures raccourcies, si on est 100% conscient que c'est une écriture raccourcie, et si on est à tout moment capable de remplacer l'écriture raccourcie par l'écriture rigoureuse.
Si on n'est pas conscient que c'est une écriture raccourcie, alors certes, c'est plus rapide à taper, mais c'est source d'erreurs.
Ici, quitte à raccourcir l'écriture, on devrait écrire :
Re: Solution particulière d'une équa diff.
mathelot a écrit:
Il ne reste plus qu'à trouver une solution particulière de l'équation:($)
Suite au post précédent, pour revenir à ton exercice, on peut chercher une solution particulière s de ($) sous la forme:
où a,b,c,d,f,g sont des réels à déterminer.
ça donne un système de six égalités à six inconnues que l'on résout aisément (facilement).
Soit
on calcule
cela conduit aux systèmes équivalents:
Une solution particulière de ($) est:
Il ne reste plus qu'à ajouter les deux solutions particulières pour obtenir une solution particulière
de l'équation initiale de l'énoncé.
Re: Solution particulière d'une équa diff.
Somme de deux solutions particulières:
soit l'équation
-3x(t)=f_1(t)+f_2(t)) (i)
(i)
où et
et  sont deux fonctions réelles.
sont deux fonctions réelles.
I désigne un intervalle de la droite réelle.
On suppose avoir une solution particulière) de
de
-3x(t)=f_1(t))
et avoir une solution particulière) de
de
-3x(t)=f_2(t))
On a:
pour tout t dans I:
- 3 \phi(t)=f_1(t))
- 3 \psi(t)=f_2(t))
on peut ajouter les deux égalités membres à membres, par linéarité on obtient:
- 3 \phi(t)+\psi'(t)- 3 \psi(t)=f_1(t)+f_2(t))
soit
' - 3(\phi+\psi)=f_1(t)+f_2(t))
donc une solution particulière de (i) définie sur I, est obtenue en sommant les deux solutions particulières.
Ici,
soit l'équation
où
I désigne un intervalle de la droite réelle.
On suppose avoir une solution particulière
et avoir une solution particulière
On a:
pour tout t dans I:
on peut ajouter les deux égalités membres à membres, par linéarité on obtient:
soit
donc une solution particulière de (i) définie sur I, est obtenue en sommant les deux solutions particulières.
Ici,
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
