bonjour tlm
est ce que quelqu'un pourra m'aider et m'expliquer ce que signifie une solution maximale sur un intervalle d'une equation differentielle?? :hein:
ce qui me gêne c'est ce nom MAXIMALE que je n'arrive pas à m'imaginer... :cry:
MErci d'avance
Solution maximale????
4 messages
- Page 1 sur 1
Une solution maximale est une solution valable sur le plus grand intervalle possible.
Par exemple : supposons que je cherche à résoudre xy' = y et que je m'y prenne mal :
je suppose que x > 0 et je sépare mes variables
y'/y = 1/ x
ln(|y|) = ln(x) + C
ln(|y|) = ln(|K|x)
|y| = |K|x est une solution de mon problème valable seulement sur ]0 ; + oo[ mais elle n'est pas maximale car la solution y = Kx est valable,elle, sur R tout entier: la première solution est une restriction de la seconde à l'intervalle ]0 ; + oo[
Par exemple : supposons que je cherche à résoudre xy' = y et que je m'y prenne mal :
je suppose que x > 0 et je sépare mes variables
y'/y = 1/ x
ln(|y|) = ln(x) + C
ln(|y|) = ln(|K|x)
|y| = |K|x est une solution de mon problème valable seulement sur ]0 ; + oo[ mais elle n'est pas maximale car la solution y = Kx est valable,elle, sur R tout entier: la première solution est une restriction de la seconde à l'intervalle ]0 ; + oo[
Bonjour,
je vais d'abord défnir le prolongement d'une solution:
soient) et
et ) deux solutions de l'équation différentielle en question, on dit que
deux solutions de l'équation différentielle en question, on dit que  prolonge
prolonge  si I
si I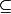 J et
J et  restreinte à I=
restreinte à I= .
.
On dit que) est maximale si on ne peut la prolonger que par elle-même.
est maximale si on ne peut la prolonger que par elle-même.
J'interprète le terme maximal comme prolongement maximal de la solution.
J'espère vous avoir éclairé,
à bientôt,
Zeb.
je vais d'abord défnir le prolongement d'une solution:
soient
On dit que
J'interprète le terme maximal comme prolongement maximal de la solution.
J'espère vous avoir éclairé,
à bientôt,
Zeb.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
