Je suis bloqué sur cette exercice :
On donne l'équation différentielle (k est une constante):
y'=y(ln(x)+K)
a) trouvez l'ensemble des solutions de l'équation différentielle
b)trouvez l'ensemble des solutions satisfaisant y(1)=1
c) trouvez la solution satisfaisant en plus de b):y'(1)=1
J'arrive du tout pas à le faire .
Si quelqu'un arrive à le faire et à me l'expliquer ça serait fort gentil merci.
Solution exercice urgent
7 messages
- Page 1 sur 1
Re: Solution exercice urgent
Exercice déjà posté hier en rubrique Secondaire
mathelot t'a répondu en te donnant ce lien :
https://fr.wikipedia.org/wiki/%C3%89quation_diff%C3%A9rentielle_lin%C3%A9aire_d%27ordre_un
Si tu l'avais lu, tu aurais :
1) résolu l'équation homogène)
( dx) s'obtient en intégrant par parties )
s'obtient en intégrant par parties )
2) cherché une solution particulière de l'équation "avec second membre"
mathelot t'a répondu en te donnant ce lien :
https://fr.wikipedia.org/wiki/%C3%89quation_diff%C3%A9rentielle_lin%C3%A9aire_d%27ordre_un
Si tu l'avais lu, tu aurais :
1) résolu l'équation homogène
(
2) cherché une solution particulière de l'équation "avec second membre"
Re: Solution exercice urgent
la forme générale des solutions est
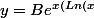-1+K)}) où B est une constante d'intégration
où B est une constante d'intégration
=1=Be^{K-1})
d'où
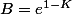
d'où
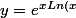})
on vérifie que=1)
d'où
d'où
on vérifie que
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
