Simplification d'une équation différentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Hymenoptera
- Messages: 2
- Enregistré le: 27 Fév 2013, 06:28
-
par Hymenoptera » 27 Fév 2013, 06:56
Bonjour,
Je souhaiterai obtenir :
}{\partial x}=0)
En partant de :
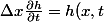u(x,t)-h(x+\Delta x, t)u(x+\Delta x,t))
J'ai commencé par faire un développement limité de :
)
et
)
:
 = u (x,t) + \Delta x \frac {\partial u}{\partial x})
 = h (x,t) + \Delta x \frac {\partial h}{\partial x})
Ce qui donne :
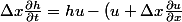 (h + \Delta x \frac {\partial h}{\partial x}))
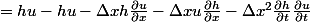
En divisant par
:
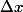
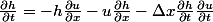
Et je m'arrête là :/ je ne sais pas comment continuer
Quelqu'un pourrait m'aider s'il vous plait =)
Merci bien,
Bonne journée à tous.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
par arnaud32 » 27 Fév 2013, 09:29
ton delta x tu le fais tendre vers 0 et tu utilises la formule de la derivee d'un produit
-
Hymenoptera
- Messages: 2
- Enregistré le: 27 Fév 2013, 06:28
-
par Hymenoptera » 27 Fév 2013, 09:34
Merci beaucoup =DD
j'avoue c'est tout simple :p
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
par DamX » 27 Fév 2013, 14:21
Hymenoptera a écrit:Merci beaucoup =DD
j'avoue c'est tout simple :p
Ou sinon directement ..
u(x+\Delta x,t)=(hu)(x+\Delta x,t)=(hu)(x,t)+\Delta x\frac{\partial (hu)}{\partial x}+o(\Delta x))
Il n'y a pas besoin de considérer les deux fonctions séparément pour ensuite reconnaitre la dérivée du produit, le produit est une fonction directement sur laquelle peut être effectué le développement limité.
Damien
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
