Bonjour, :hein:
Je recherche à simplifier une équation
J'essaie d'avoir une valeur B en fonction d'une valeur A
> qui pourrait être du type B= A*(....)
Voici mon équation:
tan(B) - B = A
avec
A est exprimé en radians
B est exprimé en radians
Merci d'avance à ceux qui pourraient m'aider.
Pour information:
La raison de cette recherche de simplification est que je voudrais pouvoir tracer une courbe de B en fonction de A avec une équation simplifiée.
(pour un système CAO)
PS: Étant nouveau sur ce site, je ne sais pas si la demande est bien adapté au site si ce n'est pas le cas, pourriez-vous m'indiquer où je pourrais m'adresser.
ViPe95 :++:
Simplification d'équation
6 messages
- Page 1 sur 1
salut,
Soit la relation F(x)=tan(x)-x=a
L'équation
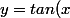) et
et 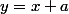 a une infinité de solutions comme on le voit
a une infinité de solutions comme on le voit
graphiquement avec la courbe représentative de la fonction tangente
dans un repère orthonormé.
sur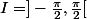
=tan(x)-x)
est dérivable,=tan^2(x)=(x+F(x))^2)
F est strictement croissante sur I.
F admet donc une bijection réciproque G définie sur
dérivable:
=tan(x)-x=a) ssi
ssi 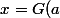)
=\frac{1}{F'(G(a))}={(G(a)+a)}^{-2})
 \left( G(a)+a \right) ^2 =1)
Soit la relation F(x)=tan(x)-x=a
L'équation
graphiquement avec la courbe représentative de la fonction tangente
dans un repère orthonormé.
sur
est dérivable,
F est strictement croissante sur I.
F admet donc une bijection réciproque G définie sur
dérivable:
Salut Vipe95,
Tu demandes la lune !
Les solutions de cette équation ne s'expriment pas avec un nombre fini de fonctions usuelles dans le cas général (sauf éventuellement pour certaines valeurs particulières de A permettant une simplification).
C'est le genre d'équation que l'on traite par calcul numérique pour obtenir un résultat numérique approché. Il existe de nombreuses méthodes pouvant donner autant de précision que l'on veut.
Autrement, la résolution formelle et exacte serait très compliquée (des genres fonctions spéciales, séries infinies).
Pour ton problème de CAO, je ne vois pas pourquoi tu aurais besoin de connaitre explicitement B en fonction de A. Pour le tracé, on se donne B que l'on fait varier, on calcule A et on marque le point (A,B), c'est à dire A sur l'axe horizontal et B sur l'axe vertical. La courbe obtenue est la représentation de B en fonction de A : c'est bien ce qui était demandé.
Tu demandes la lune !
Les solutions de cette équation ne s'expriment pas avec un nombre fini de fonctions usuelles dans le cas général (sauf éventuellement pour certaines valeurs particulières de A permettant une simplification).
C'est le genre d'équation que l'on traite par calcul numérique pour obtenir un résultat numérique approché. Il existe de nombreuses méthodes pouvant donner autant de précision que l'on veut.
Autrement, la résolution formelle et exacte serait très compliquée (des genres fonctions spéciales, séries infinies).
Pour ton problème de CAO, je ne vois pas pourquoi tu aurais besoin de connaitre explicitement B en fonction de A. Pour le tracé, on se donne B que l'on fait varier, on calcule A et on marque le point (A,B), c'est à dire A sur l'axe horizontal et B sur l'axe vertical. La courbe obtenue est la représentation de B en fonction de A : c'est bien ce qui était demandé.
Salut mathelot,
inutile d'aller chercher midi à quatorze heures !
Il s'agit d'un problème de représentation graphique de fonction réciproque.
La fonction donnée est :
A(B) = tan(B) - B
Trace classiquement la courbe représentative de tan(B) - B = A , mais en portant B sur l'axe des ordonnées et A sur l'axe des abscisses. Il est alors évident que cette même courbe, regardée maintenant comme B(A), puisque A est sur l'axe des abscisses et B sur celui des ordonnées, est aussi la représentation de la fonction réciproque B(A).
inutile d'aller chercher midi à quatorze heures !
Il s'agit d'un problème de représentation graphique de fonction réciproque.
La fonction donnée est :
A(B) = tan(B) - B
Trace classiquement la courbe représentative de tan(B) - B = A , mais en portant B sur l'axe des ordonnées et A sur l'axe des abscisses. Il est alors évident que cette même courbe, regardée maintenant comme B(A), puisque A est sur l'axe des abscisses et B sur celui des ordonnées, est aussi la représentation de la fonction réciproque B(A).
[font=Times New Roman]Bonsoir,[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Il semblerait qu'il nait de solution simple à ma question.[/size][/font]
[font=Times New Roman]Merci mathelot et JJa, d'être pencher sur mon problème.[/font]
[font=Times New Roman]Je vais essayer une autre voie.[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Pour information (si vous êtes curieux):[/size][/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]J'essaye de tracer une courbe (une développante de cercle) dans un logiciel CAO.[/size][/font]
[font=Times New Roman]Mais mon logiciel CAO ne sait tracer une courbe (avec équation) selon un abscisse rectiligne ou curviligne seulement. Hors toutes les formules que j'ai pu trouver sur les développantes de cercle n'utilise pas ce principe (mais Coordonnées polaire, ...)[/font]
[font=Times New Roman]
Donc je cherche de trouver une solution et[/font]
[font=Times New Roman]pour cela j'ai récupéré quelques formules qui sont utiliser pour décrire la courbe dont
celle de mon sujet tan(B) - B = A (appeler involute de l'angle B)[/font]
[font=Times New Roman]
Cette formule est indiqué dans un livre (traité théorique et pratique des engrenages) - On l'utilise pour les développantes de cercle dans les engrenages.[/font]
[font=Times New Roman]
Voici graphiquement, ce que je cherche à faire.[/font]
[url="http://blog.iquebec.com/roi.vico/blogimage.php?t=0&i=614609"]http://blog.iquebec.com/roi.vico/blogimage.php?t=0&i=614609[/url]
[font=Times New Roman][font=Verdana][size=2]
[/font]La droite L est tangente au cercle et perpendiculaire à OT[/size][/font]
[font=Times New Roman]
[/font][font=Times New Roman]Jessaie dexprimer la longueur IM en fonction de R et la longueur de larc IP[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Je connais :
- Le rayon R > imposé[/size][/font]
[font=Times New Roman]- La longueur de larc IP > mon abscisse curviligne[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Je sais :[/size][/font]
[font=Times New Roman]- La longueur de larc TP est égal à L (cest le principe de la développante de cercle)[/font]
[font=Times New Roman]- Tan(B) B = A (avec A et B en Radian) >> indiqué dans le livre.[/font]
[font=Times New Roman]- OM = OI+IM = R + IM[/font]
[font=Times New Roman]- OM = R / cos (B)[/font]
[font=Times New Roman]- La longueur de larc IP = (;) x R x A)/180 (avec A en degrés)[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]alors [/size][/font]
[font=Times New Roman]Jai commencé par exprimé A par la longueur de larc IP[/font]
[font=Times New Roman]> A= (IP x 180) / (;) x R) en degrés[/font]
[font=Times New Roman]En radians => A= IP / R
puis [/font]
[font=Times New Roman]> Tan(B) B = IP / R (Cest là que je bloque)[/font]
[font=Times New Roman]
Si javais une équation du type B= ..
Je pourrais linsérer dans la formule OM = R / cos (B)
Voila la raison de ma demande.
Encore merci.
@+
ViPe95 [/font]
[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Il semblerait qu'il nait de solution simple à ma question.[/size][/font]
[font=Times New Roman]Merci mathelot et JJa, d'être pencher sur mon problème.[/font]
[font=Times New Roman]Je vais essayer une autre voie.[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Pour information (si vous êtes curieux):[/size][/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]J'essaye de tracer une courbe (une développante de cercle) dans un logiciel CAO.[/size][/font]
[font=Times New Roman]Mais mon logiciel CAO ne sait tracer une courbe (avec équation) selon un abscisse rectiligne ou curviligne seulement. Hors toutes les formules que j'ai pu trouver sur les développantes de cercle n'utilise pas ce principe (mais Coordonnées polaire, ...)[/font]
[font=Times New Roman]
Donc je cherche de trouver une solution et[/font]
[font=Times New Roman]pour cela j'ai récupéré quelques formules qui sont utiliser pour décrire la courbe dont
celle de mon sujet tan(B) - B = A (appeler involute de l'angle B)[/font]
[font=Times New Roman]
Cette formule est indiqué dans un livre (traité théorique et pratique des engrenages) - On l'utilise pour les développantes de cercle dans les engrenages.[/font]
[font=Times New Roman]
Voici graphiquement, ce que je cherche à faire.[/font]
[url="http://blog.iquebec.com/roi.vico/blogimage.php?t=0&i=614609"]http://blog.iquebec.com/roi.vico/blogimage.php?t=0&i=614609[/url]
[font=Times New Roman][font=Verdana][size=2]
[/font]La droite L est tangente au cercle et perpendiculaire à OT[/size][/font]
[font=Times New Roman]
[/font][font=Times New Roman]Jessaie dexprimer la longueur IM en fonction de R et la longueur de larc IP[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Je connais :
- Le rayon R > imposé[/size][/font]
[font=Times New Roman]- La longueur de larc IP > mon abscisse curviligne[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]Je sais :[/size][/font]
[font=Times New Roman]- La longueur de larc TP est égal à L (cest le principe de la développante de cercle)[/font]
[font=Times New Roman]- Tan(B) B = A (avec A et B en Radian) >> indiqué dans le livre.[/font]
[font=Times New Roman]- OM = OI+IM = R + IM[/font]
[font=Times New Roman]- OM = R / cos (B)[/font]
[font=Times New Roman]- La longueur de larc IP = (;) x R x A)/180 (avec A en degrés)[/font]
[font=Times New Roman][font=Verdana][size=2]
[/font]alors [/size][/font]
[font=Times New Roman]Jai commencé par exprimé A par la longueur de larc IP[/font]
[font=Times New Roman]> A= (IP x 180) / (;) x R) en degrés[/font]
[font=Times New Roman]En radians => A= IP / R
puis [/font]
[font=Times New Roman]> Tan(B) B = IP / R (Cest là que je bloque)[/font]
[font=Times New Roman]
Si javais une équation du type B= ..
Je pourrais linsérer dans la formule OM = R / cos (B)
Voila la raison de ma demande.
Encore merci.
@+
ViPe95
 [/font]
[/font]
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
