Bonjour,
J'ai une question qui me gene et j'ai besoin d'un coup de pouce, n'hésitez pas de me donner votre avis concernant le raisonnement que je vais faire et surtout une idée concernant la question que je poserai.
On se donne l'opérateur intégrale

défini par:
(x)=\int_{D}e^{icx.y}f(y)dy)
où
,)
)
sont deux points de
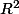
,

et
\in R^{2}; x_{1}^{2} +x_{2}^{2}\leq 1\})
est le disque unité de

Il est bien claire que l'opérateur

est un opérateur de Hilbert Schmidt et par conséquent il admet une infinité dénombrable de fonction propres qui forment une base de
)
. Ma question porte sur la simplicité des valeurs propres des fonctions propres de

. C'est à dire si je me donne une fonction propre g de

dont la valeur propre est

. La question est:

est elle simple?
Merci bien davantage pour vos remarques et commentaires.
