Simple suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 26 Jan 2010, 13:11
par Near » 26 Jan 2010, 13:11
salut :id:
On considere la suite
)
définie par
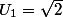
et pour tout
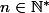
.
[CENTER]
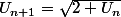
[/CENTER]
1) Montrer en raisonnant par récurrence que cette suite est majorée par 2.
2)Montrer que
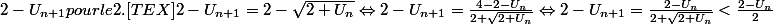
je peux pas dire que la suite converge vers 2.
merci.
-
Helidjah
- Membre Naturel
- Messages: 12
- Enregistré le: 26 Jan 2010, 11:15
-
 par Helidjah » 26 Jan 2010, 16:35
par Helidjah » 26 Jan 2010, 16:35
Salut
Il faut passer à la limite dans ton inégalité : les inégalités strictes deviennent des inégalités larges.
Ainsi, si on note
=\lim(U_n)=l)
, on a :
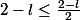
.
Or,
)
est positive et majorée par 2. Donc
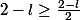
.
D'où
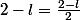
.
On en déduit que
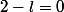
i.e
=2)
.
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 26 Jan 2010, 16:49
par Near » 26 Jan 2010, 16:49
Helidjah a écrit:Salut
Il faut passer à la limite dans ton inégalité : les inégalités strictes deviennent des inégalités larges.
Ainsi, si on note
=\lim(U_n)=l)
, on a :
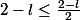
.
Or,
)
est positive et majorée par 2. Donc
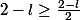
.
D'où
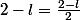
.
On en déduit que
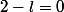
i.e
=2)
.
merci :id:
question : comment as-tu obtenu cette résultat,
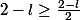
?
:briques:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Jan 2010, 16:52
par Ben314 » 26 Jan 2010, 16:52
Salut,
il me semble qu'il y a un petit soucis dans la méthode d'Helidjah :
avant d'écrire : "si on note
=\lim(U_n)=l)
" , Il faudrait justifier que cette limite existe bel et bien....
Si on veut garder cette idée, il faudrait par exemple montrer que la suite est croissante ce qui, vu qu'elle est majorée montrerait que la limite existe.
A mon avis, vu la question précédente, ce n'est pas la solution attendue.
Je pencherai plus pour une récurrence :
Partant de la formule
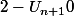
on conclue en utilisant le théorème des gendarmes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Helidjah
- Membre Naturel
- Messages: 12
- Enregistré le: 26 Jan 2010, 11:15
-
 par Helidjah » 26 Jan 2010, 16:59
par Helidjah » 26 Jan 2010, 16:59
)
est majorée par 2 sous-entend que
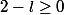
. Or la fonction
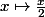
est inférieure à l'identité
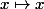
sur

.
Donc
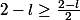
.
Comme le fait remarquer Ben314, il faut nécessairement montrer que la suite est croissante. Désolé pour le manque de rigueur.
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 26 Jan 2010, 17:51
par Near » 26 Jan 2010, 17:51
merci pour vous :id: .
@ "Ben314" je sais pas comment commencer la méthode que tu m'as suggérée :triste:
est-ce que tu peux encore m'aider :id:
merci.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Jan 2010, 18:03
par Ben314 » 26 Jan 2010, 18:03
Si tu applique succésivement la propriété
<\frac{1}{2}\times\frac{1}{2}(2-U_1))
.
.
.
Je te laisse chercher la suite, puis démontrer proprement le résultat à l'aide d'une récurrence
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 26 Jan 2010, 19:50
par Near » 26 Jan 2010, 19:50
Ben314 a écrit:Si tu applique succésivement la propriété
<\frac{1}{2}\times\frac{1}{2}(2-U_1))
.
.
.
Je te laisse chercher la suite, puis démontrer proprement le résultat à l'aide d'une récurrence
hmm :hum: ,pour n=1,on a
\Leftrightarrow \frac{1}{2+\sqrt{2+\sqrt{2}}}< \frac{1}{2})
ce qui est vrai.
maintenant je suppose que la propriété est vrai au rang

et je montre qui l'est au rang

.
\Leftrightarrow \frac{1}{2+\sqrt{2+\sqrt{u_{n+1}}}}< \frac{1}{2})
ce qui est vrai.
j'ai peut être pas répondu a ta question :triste: ,mais c'est tout ce que je peux faire.

.
merci "Ben314"

.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Jan 2010, 20:11
par Ben314 » 26 Jan 2010, 20:11
n=1 =>
<\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}(2-U_1))
et on montre facilement (récurrence) que
^{n-1}(2-U_1))
Or
^{n-1})
tend vers 0 et
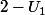
est une constante (on se fiche de combien elle vaut...) donc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 26 Jan 2010, 20:16
par nodgim » 26 Jan 2010, 20:16
Juste en aparté pour la preuve de la croissance de la suite:
rac(2+rac(2+rac(2.... s'écrit de gauche à droite ou de droite à gauche.
Or, si on l'écrit de gauche à droite, on ajoute toujours, donc la suit croît.
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 26 Jan 2010, 21:57
par Near » 26 Jan 2010, 21:57
Ben314 a écrit:n=1 =>
<\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}(2-U_1))
et on montre facilement (récurrence) que
^{n-1}(2-U_1))
Or
^{n-1})
tend vers 0 et
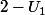
est une constante (on se fiche de combien elle vaut...) donc...
donc

converge vers 2 :++: .
merci

100000 "Ben314" :id: :id:
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 26 Jan 2010, 21:58
par Near » 26 Jan 2010, 21:58
nodgim a écrit:Juste en aparté pour la preuve de la croissance de la suite:
rac(2+rac(2+rac(2.... s'écrit de gauche à droite ou de droite à gauche.
Or, si on l'écrit de gauche à droite, on ajoute toujours, donc la suit croît.
merci "nodgim" :id: :id: .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
<\frac{1}{2}\times\frac{1}{2}(2-U_1))