Similitudes

[jeje56]

Bonjour,

Soit ABC un triangle direct. On construit le triangle A'BA direct rectangle isocèle en A' et le triangle A''AC direct rectangle isocèle en A''. On note I le milieu de [BC].

Montrer que les droite (IA') et (IA'') sont orthogonales en utilisant les similitudes.

Je ne vois pas par où commencer... Merci bcp de votre aide !

[yos]

Regarde la composée

(nature, effet sur B,...).

[yos]

Autre méthode (plus moche) avec un ROD d'origine A :
B(b), C(c), A'(a'), A''(a'')
A' est l'image de A par la similitude directe de centre B, d'angle pi/4, de rapport donc a'=b(1-i)/2. De même a''=...
Puis ...

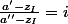
[yos]

Troisième méthode.

la similitude directe de centre C, d'angle pi/4, de rapport .
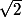
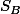
la similitude directe de centre B, d'angle pi/4, de rapport .
est une rotation d'angle pi/2qui envoie E sur D. De plus on voit qu'elle fixe I, donc c'est son centre. On a donc (IE,ID)=pi/2.
(et accessoirement IE=ID).

[jeje56]

Salut Yos, merci pour ces réponses, j'étudie ça demain ! ;-)

[jeje56]

Regarde la composée

(nature, effet sur B,...).

Salut,
Je trouve que la composé est la symétrie de centre I, transformant B en C ; comment en déduire l'orthogonalité des droites (IA') et (IA'') ?

Ok pour la méthode 3

Merci !

[yos]

Je trouve que la composé est la symétrie de centre I, transformant B en C ; comment en déduire l'orthogonalité des droites (IA') et (IA'') ?

En appelant J l'image de I par la première rotation (), tu as aussi et donc deux triangles isocèles rectangles de même hypoténuse...

[jeje56]

Bien vu ;-) On obtient un carré... Merci yos !

[jeje56]

Autre méthode (plus moche) avec un ROD d'origine A :
B(b), C(c), A'(a'), A''(a'')
A' est l'image de A par la similitude directe de centre B, d'angle pi/4, de rapport donc a'=b(1-i)/2. De même a''=...
Puis ...

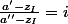
et non A, non ?

Ou alors : A' image de B par la même similitude de centre A...

[yos]

Oui en effet. Je corrige.

[jeje56]

Oui en effet. Je corrige.

En fait, la similitude que tu as utilisée pour trouver a' est celle de centre A qui transforme A' en B, de rapport racine(2) (il me semble...)

[Ben314]

En fait, la similitude que tu as utilisée pour trouver a' est celle de centre A qui transforme A' en B, de rapport racine(2) (il me semble...)

Quelle que soit la méthode utilisée, cela ne change (évidement) pas l'affixe a' de A' :
Centre B, angle , rapport : A->A' donc
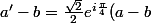Centre A, angle , rapport : A'->B donc
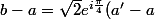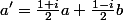
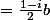
Dans les deux cas, on trouve [ si on a pris ]

[jeje56]

C'est vrai... Merci ;-)