Ça sert à quelque chose ?

[adrien69]

Une méthode analytique.

On sait que exp est croissante car positive et de dérivée elle-même.

Dans ce cas pas de limite=majorée.

Supposons donc exp majorée et prenons la borne sup M sur R+.

Alors par croissance et définition du sup, si on se prend M/2 il existe T tel que pour tout x>T,
Sauf que .

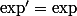
Donc dès que x>T.

Et ça c'est absurde vu que R est archimédien (Yeah placé deux fois en deux jours !) et qu'on avait supposé exp majorée

[adrien69]

Autre démo via ce que tu avais fait avant sur les puissances et l'exponentielle.

On suppose qu'on a montré que exp(x)=exp(1)^x dès que x est un entier naturel. Et qu'on a de plus exp positive. Donc croissante.
Revenons aux réels.

Dès lors, on sait que comme exp'(0)>0, pour tout x>0, exp(x)>1 (on a une stricte croissance locale plus une croissance globale + continuité de la dérivée, je te laisse bien mettre les arguments)

En particulier exp(1)>0.

Sauf que exp(n)=exp(1)^n qui tend donc vers l'infini. Donc par croissance, exp(x) tend vers l'infini.

[adrien69]

Allez, j'ai envie de faire exotique...

On va plutôt regarder ln.

Si on sait que exp est continue strictement croissante, ln existe, et le théorème de dérivation des réciproques assure que :

ln'(x) existe et vaut 1/x pour x>0

Donc (x-ln(x))'=1-1/x ce qui est positif dès que x>=1.

Donc x-ln(x) est croissant au delà de 1.

Sauf que en 1, ça vaut 1. Donc x>ln(x) dès que x est plus grand que 1.

Comme l'exponentielle est strictement croissante, composer par elle ne change pas les inégalités,

Et donc exp(x)>x dès que x est supérieur à 1.

[adrien69]

Oui, je suis en stage, sur le campus de Besançon, et donc je n'ai rien d'autre à faire que de trouver 10 démos pour un exo de Sup.

[Trident]

Oula ! Merci pour toutes ces méthodes. Celle du lemme de Gronwall me plaît particulièrement car ça faisait assez longtemps que je l'avais pas utilisé et donc oublié. Concernant la méthode analytique, j'y avais pensé !
Celle avec les puissances me plaît aussi beaucoup car je peux l'inclure dans ma fiche juste après la démonstration de exp(x)=exp(1)^x pour x rationnel.
Celle avec le log est pas mal car fait bien réviser le théorème de dérivation des réciproques.

J'en rajoute une histoire de citer le théorème des accroissements finis (car ça ressemble dejà à ce qu'on a fait).

Soit x > 0 (dans un voisinage de +oo). La fonction exp est continue sur [0;x] et dérivable sur ]0;x[ (par hypothèses) donc d'après le TAF, il existe c dans ]0;x[ tel que exp(x)-exp(0)= exp'(c)(x-0). Ceci se réécrit, exp(x)=1+ exp(c)x. Et comme exp > 0, ça conclut le tout.

[adrien69]

Soit x > 0 (dans un voisinage de +oo). La fonction exp est continue sur [0;x] et dérivable sur ]0;x[ (par hypothèses) donc d'après le TAF, il existe c dans ]0;x[ tel que exp(x)-exp(0)= exp'(c)(x-0). Ceci se réécrit, exp(x)=1+ exp(c)x. Et comme exp > 0, ça conclut le tout.

Ouais, je me suis dit que je n'allais pas la mettre vu qu'elle était identique à celle sur la convexité. Je pense en avoir encore une dans le chapeau, mais elle me semble tirée par les cheveux et je ne suis pas bien sûr que ce soit correct et/ou utile.


PS : Ah oui mais non, attention ! avec ta façon de faire ça ne marche pas. Dans ta façon d'écrire c dépend de x.

Il est donc bien plus utile d'utiliser l'inégalité des accroissements finis. Essaie de bien le rédiger.

Ou sinon il faut dire que exp(c) est toujours plus grand que 1 par croissance.

[Trident]

Ouais, je me suis dit que je n'allais pas la mettre vu qu'elle était identique à celle sur la convexité. Je pense en avoir encore une dans le chapeau, mais elle me semble tirée par les cheveux et je ne suis pas bien sûr que ce soit correct et/ou utile.

Si t'as le temps de la taper, je suis preneur. :we:

[adrien69]

J'ai tout le temps, je m'emmerde.

Ici on utilise exp strictement croissante et continue.

Quand on a f : R-> R+ continue strictement croissante et g sa réciproque sur l'image de f,

On a toujours f, ou g ou les deux qui tendent vers l'infini (évident, mais pourquoi ?)

Donc là on va comparer exp à sa réciproque : ln
sur R*+

h(x)=exp(x)-ln(x)

h'(x)=exp(x)-1/x

ce qui est positif dès que x est supérieur à 1 puisque exp est croissante

Donc h est croissante à partir de 1, sauf que h(1)=e

Donc exp(x) >=ln(x)+e pour tout x.

Donc finalement, dans tous les cas (et même si ln ne tendait pas vers l'infini), exp tend vers l'infini (pourquoi ?)


(Je ne pense pas que ce soit une méthode générale par contre)

[Trident]

Quand on a f : R-> R+ continue strictement croissante et g sa réciproque sur l'image de f,

On a toujours f, ou g ou les deux qui tendent vers l'infini (évident, mais pourquoi ?)

Si je me prend une fonction f : R -> R+ continue strictement croissante et majorée par un certain réel M > 0. Dans ce cas, l'image de R par f est incluse dans [0;M] donc la réciproque g est définie sur un truc inclus dans [0;M] donc du coup, on peut plus parler de limite lorsque x tend vers +oo de g(x) ?

[adrien69]

Si je me prend une fonction f : R -> R+ continue strictement croissante et majorée par un certain réel M > 0. Dans ce cas, l'image de R par f est incluse dans [0;M] donc la réciproque g est définie sur un truc inclus dans [0;M] donc du coup, on peut plus parler de limite lorsque x tend vers +oo de g(x) ?

Oups ! oui, il fallait entendre "quand on tend vers l'extrémité de l'intervalle de définition".

[Trident]

Car en fait, on a pas beaucoup d'informations sur ln, on sait que son ensemble de définition, c'est exp(R) et on ne sait pas que ça vaut nécessairement R+ donc à priori, on n'a pas le droit de parler de limite en +oo de ln(x). Pour cela, il faudrait montrer que exp : R -> R+ est surjective (donc bijective...).

Dans ce cas, c'est rapide. Si exp ne tend pas vers +oo quand x tend vers +oo, alors comme exp est croissante, elle est majorée par un réel M > 0.

Mais alors, M+1 > 0 et donc il existe y dans R tel que exp(y)=M+1, cela contredit le fait que M est un majorant.

Reste à montrer que exp : R -> R+ est surjective.

EDIT : OK pour le rectificatif.

[adrien69]

Non en fait la dernière preuve se mort la queue. Oublie. Je te l'avais dit que je n'étais pas bien sûr.

[adrien69]

C'est simple, le domaine c'est R+ si et seulement si exp tend vers l'infini, je me suis emmêlé les pinceaux sévèrement là.

[Trident]

En effet. En tout cas, merci pour les différentes preuves, c'est toujours bon pour l'entraînement.

[adrien69]

Une autre façon de faire avec les accroissements finis :

exp ne tend pas vers l'infini si et seulement si elle a une limite puisque croissante. On l'appelle l.

On a dès lors exp(x+1)-exp(x) qui tend vers 0 en l'infini.

Mais on peut trouver c(x) entre x et x+1 tel que exp(x+1)-exp(x)=exp(c(x))

Clairement c(x)->+oo puisque plus grand que x.

Mais exp(c(x)) tend vers 0. Donc l=0, ce qui est absurde puisque exp est croissante et exp(0)=1.

[adrien69]

Si tu vois d'autres méthodes préviens hein.

[Trident]

Une autre façon de faire avec les accroissements finis :

exp ne tend pas vers l'infini si et seulement si elle a une limite puisque croissante. On l'appelle l.

On a dès lors exp(x+1)-exp(x) qui tend vers 0 en l'infini.

Mais on peut trouver c(x) entre x et x+1 tel que exp(x+1)-exp(x)=exp(c(x))

Clairement c(x)->+oo puisque plus grand que x.

Mais exp(c(x)) tend vers 0. Donc l=0, ce qui est absurde puisque exp est croissante et exp(0)=1.

Bravo encore une fois pour cette méthode.

Si tu vois d'autres méthodes préviens hein.

Je pense que je vais m'arrêter là du coup. :ptdr: Mais si, en résolvant un exercice sur la dérivabilité, je vois une autre démo sortie de nulle part, je n'hésiterai pas!

[adrien69]

Utiliser le schéma en haut à droite là http://fr.wikipedia.org/wiki/Fonction_hyperbolique ça doit aussi être faisable mais ça doit être un peu plus malin/compliqué (ça donne une définition géométrique de l'exponentielle, comme ch+sh, et la définition de ces deux là comme projetés leur donne presque clairement la limite infinie)

Il y a aussi moyen que ça se morde la queue. À vérifier.

[adrien69]

Formule de Taylor-Lagrange avec reste intégral. Ça te donne tout d'un seul coup en fait : positivité et minoration par la somme de Taylor.

[Trident]

Ouais méthode sophistiquée, j'aime!