Series de Taylors...

[pouik]

Bonjour,
Pourriez-vous m'aider à résoudre ce petit exo auquel je ne comprends rien. Merci d'avance pour votre aide.

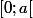
Soit une application de classe sur un intervalle (avec ) et vérifiant

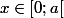
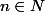
Pour et , on note .
1. Prouver la relation .
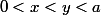
2. Pour tout couple tel que et tout entier naturel , montrer que

3. En déduire que est la somme de sa série de Taylor sur .

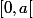
[pouik]

Pour la quaestion 1., ca me fait penser à la formule de Taylor avec reste intégrale, mais je ne vois pas bien comment l'exploiter ! avez vous des idées ?

Merci d'avance.

[ThSQ]

Ouais c'est Taylor avec reste intégral (f(x) = f(0) + ...) + changement de variable t = x*u

2 : f^(n) est une fonction croissante

[pouik]

Ouais c'est Taylor avec reste intégral (f(x) = f(0) + ...) + changement de variable t = x*u

2 : f^(n) est une fonction croissante

Merci mais à quoi correspond la fonction f ?
Sinon dois-je justifier le changement de variable ? ou puis-je me contenter de dire que l'on obtient le resultat escompté en posant le changement de variable ...

[ThSQ]

Merci mais à quoi correspond la fonction f ?
Sinon dois-je justifier le changement de variable ? ou puis-je me contenter de dire que l'on obtient le resultat escompté en posant le changement de variable ...

f = h, sorry.

Le changt de variable se justifie comme d'hab (ici tout est C^°°)