Séries

par **rifly01** » 06 Oct 2007, 05:19

Bonjour,

Quelqu'un pourrait me dire comment montrer la convergence uniforme ?

Merci

par **rifly01** » 06 Oct 2007, 07:00

Je donne un exemple.

Si on veut montrer que la fonction

converge uniformément sur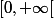

.

- Convergence ponctuelle sur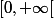

:

quand x tend vers + infini.

- Convergence uniforme sur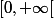

:
On doit calculer

On considère la fonction

et donc le signe de f' est celui de (1-nx)
En faisant le tableau de variations ... on trouve que le maximum est atteint en x=1/n et f(1/n)=1/(ne)

Donc

Ainsi, f_n converge uniformément vers 0 sur [0, +inf[.

Est-ce une bonne méthode ?
Est-elle juste, sinon merci de me corriger.

par **fahr451** » 06 Oct 2007, 07:29

bonjour
rien à redire

par **rifly01** » 06 Oct 2007, 12:50

Bonjour,
C'est à dire que c'est bien ?

par **fahr451** » 06 Oct 2007, 12:53

ben oui c'est très bien même

20/20
note que le calcul des variations n'est pas toujours possible

et on passe alors par des convergences normales (locales)

par **rifly01** » 06 Oct 2007, 13:03

Justement, là est mon problème.
Moi je connais que cette méthode et donc je l'applique machinalement...
Dans quelle cas, je ne peux pas l'appliquer ?

par **fahr451** » 06 Oct 2007, 13:16

quand les variations sont difficiles

par **rifly01** » 06 Oct 2007, 13:31

Il y a des cas simples ou on peut répondre (sans rien faire, cas évidents) ?

par **fahr451** » 06 Oct 2007, 13:42

question délicate
qu'est ce qui est évident?
donne des exemples et je t'aiderai

par **rifly01** » 06 Oct 2007, 16:04

Par exemple :

par **fahr451** » 06 Oct 2007, 16:09

oui que trouves tu ?

par **rifly01** » 06 Oct 2007, 17:00

Re -

Pour cette fonction j'ai deux réponse.

Travaillons dans R+

La première
------

tend vers

lorsque x tend vers

.

De ce fait, il y a ni convergence simple ni convergence uniforme (ni normale).

La deuxième
------

tend vers x lorsque n tend vers

Donc, f_n converge ponctuellement vers f(x)=x sur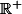

(même R)

On considère

.

g_n est croissante et non majorée sur R+

Donc

donc pas de convergence uniforme sur R+.

J'ai deux réponses parce que je ne fais pas varier la même variable.
Doit-on toujours varier la même variable ?

par **fahr451** » 06 Oct 2007, 17:04

rifly01 a écrit:Re -

Pour cette fonction j'ai deux réponse.

Travaillons dans R+

La première
------
tend vers lorsque x tend vers .

De ce fait, il y a ni convergence simple ni convergence uniforme (ni normale).

------
tend vers x lorsque n tend vers
Donc, f_n converge ponctuellement vers f(x)=x sur (même R)

.

deux réponses contradictoires

on garde laquelle ?

par **rifly01** » 06 Oct 2007, 17:05

Oui,
On garde la deuxième vu qu'elle est plus développée, non ?

par **fahr451** » 06 Oct 2007, 17:07

heu
on garde ce qui est juste développé ou pas

tu dis:
1 blanc pas de convergence simple
et

2 noir convergence ponctuelle = simple
c'est blanc ou noir ?

par **rifly01** » 06 Oct 2007, 17:09

Je choisis le noir, c'est mon dernier mot. (JP)

par **fahr451** » 06 Oct 2007, 17:11

ben oui

fixer n et faire varier x n' aucun intérèt pour la convergence

ensuite ce que tu dis sur g est correct

y a t il une convergence uniforme locale ?

par **rifly01** » 06 Oct 2007, 17:16

Localement : [0, A]

Oui puisque le sup de g_n vaut g_n(A)=f_n(A)-A
Et si on fait tendre n vers +inf, on a bien 0,

Donc f_n converge uniformément vers x sur [0,A] (localement)

par **rifly01** » 06 Oct 2007, 19:12

C'est bon j'espère ?

par **fahr451** » 06 Oct 2007, 19:25

oui c'est bon si tu as fait les variations de gn
sinon c 'est bon par un théorème de dini

Séries

Séries

Qui est en ligne