Series numériques hellpppppp
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
amaniis
- Messages: 9
- Enregistré le: 27 Sep 2017, 17:28
-
 par amaniis » 27 Sep 2017, 18:54
par amaniis » 27 Sep 2017, 18:54

bonjour tout le monde on vient de faire le cours mais histoire d'être a jour je voulais révisé les exemples qu'on a fait pendant le cours mais là je suis bloquée

question : étudier la nature de la série de terme général 1/n(n+1)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 27 Sep 2017, 18:57
par chan79 » 27 Sep 2017, 18:57
salut
un indice

-
amaniis
- Messages: 9
- Enregistré le: 27 Sep 2017, 17:28
-
 par amaniis » 27 Sep 2017, 19:03
par amaniis » 27 Sep 2017, 19:03
je me demande est ce qu'il faut toujours étudier la nature de la suites de sommes partielles ou des fois il suffit de savoir si le terme générale de la séries dans ce cas la suite de terme générale 1/n(n+1) si elle tend vers 0 quand n tend vers +00 alors la série est convergente car la suites des sommes partielles est convergentes

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Sep 2017, 19:45
par Ben314 » 27 Sep 2017, 19:45
Salut,
amaniis a écrit:...il suffit de savoir si le terme générale de la séries dans ce cas la suite de terme générale 1/n(n+1) si elle tend vers 0 quand n tend vers +00 alors la série est convergente car la suites des sommes partielles est convergentes
ça, ben c'est justement LE truc faux par excellence : si le terme général d'une suite tend vers 0, ben ça prouve pas du tout que la série en question est convergente.
Exercice : On considère une série telle que les somme partielles d'ordre

soient

(ou n'importe quoi d'autre qui tend vers l'infini "lentement").
a) La série est-elle convergente ?
b) Quel est le terme général

de cette série ?
c) Vers quoi tend

lorsque
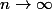
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités

