Series de fonctions et Reste
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fidelcastro
- Messages: 7
- Enregistré le: 10 Juin 2006, 18:58
-
 par fidelcastro » 10 Juin 2006, 19:04
par fidelcastro » 10 Juin 2006, 19:04
Je m'entraine sur quelques planches d oraux et je bloque sur une de ces questions :
j ai une serie de fonction avec un(x) = anx^n*(1-x)
avec an decroissante et positive
ici x appartient a [0,1]
on pose vn= sup l Rn(x) l avec Rn le reste d ordre n
on me demande de montrer que si lim an =0 alors (vn) converge vers 0
Peut etre pourriez vous m aidez sachant qu il faut surement majorer cette expression je vous remercie
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Juin 2006, 19:10
par yos » 10 Juin 2006, 19:10
On montre la double-inclusion. De gauche à droite c'est évident (et toujours vrai sans hypothèses particulières sur f et g). De droite à gauche, on utilise l'égalité fgf=f : c'est presque immédiat.
-
mathelot
 par mathelot » 10 Juin 2006, 19:55
par mathelot » 10 Juin 2006, 19:55
Le but de l'exercice est de montrer que la suite de fonctions
)
tend ponctuellement vers la fonction nulle.
=\lim R_{n}(1)=0)
.
Pour x fixé

, on a la majoration suivante:
 \leq a_{n} (1-x) \sum_{k>=n}x^{k})
, la suite
)
étant positive , décroissante et le dernier facteur
est le reste d'une série géométrique convergente.
-
fidelcastro
- Messages: 7
- Enregistré le: 10 Juin 2006, 18:58
-
 par fidelcastro » 10 Juin 2006, 20:07
par fidelcastro » 10 Juin 2006, 20:07
On me demande ensuite d'etudier la reciproque , ne faudrait t il pas raisonner par l absurde en posant que lim an different de zero?
-
mathelot
 par mathelot » 10 Juin 2006, 20:39
par mathelot » 10 Juin 2006, 20:39
et puis finalement, comme Rn est une suite de fonctions continues
qui tend vers zero simplement en décroissant sur le compact [0;1],
elle tend uniformément vers zéro (Dini).
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Juin 2006, 20:50
par yos » 10 Juin 2006, 20:50
J'avais pourtant posté mon précédent message sur un autre fil!
Sur celui-ci, c'est amusant aussi remarquez.
-
mathelot
 par mathelot » 10 Juin 2006, 20:59
par mathelot » 10 Juin 2006, 20:59
oui, c'est incroyable, votre réponse s'appliquait à deux questions distinctes ?
-
mathelot
 par mathelot » 10 Juin 2006, 21:23
par mathelot » 10 Juin 2006, 21:23
si
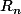
tend uniformémemnt vers la fonction nulle sur [0;1]
alors la série converge uniformément sur [0;1] vers sa limite et en particulier
pour la valeur x=1/2.
D'où
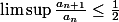
et donc
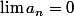
-
fidelcastro
- Messages: 7
- Enregistré le: 10 Juin 2006, 18:58
-
 par fidelcastro » 10 Juin 2006, 21:45
par fidelcastro » 10 Juin 2006, 21:45
Pourquoi la serie converge particulierement pour x =1/2?
-
mathelot
 par mathelot » 10 Juin 2006, 23:00
par mathelot » 10 Juin 2006, 23:00
La réciproque peut se montrer par l'absurde:
)
étant positive,décroissante est convergente.
supposons sa limite

.
alors:
 x^{n} \leq V_{n}(x) \leq \epsilon)
en faisant tendre x vers 1,

d'où une contradiction si l > 0.
-
fidelcastro
- Messages: 7
- Enregistré le: 10 Juin 2006, 18:58
-
 par fidelcastro » 11 Juin 2006, 09:38
par fidelcastro » 11 Juin 2006, 09:38
D'accord c'est sympa je vous remercie de votre aide
-
fidelcastro
- Messages: 7
- Enregistré le: 10 Juin 2006, 18:58
-
 par fidelcastro » 11 Juin 2006, 09:46
par fidelcastro » 11 Juin 2006, 09:46
Ce que je voudrais savoir c'est quand est ce qu'intervient l'hypothese que vn converge vers 0?
-
mathelot
 par mathelot » 11 Juin 2006, 10:20
par mathelot » 11 Juin 2006, 10:20
Dans la réciproque, on traduit l'hypothèse:
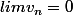
par:
 \leq \epsilon)
puisque
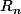
est une suite de fonctions positives tendant
uniformément vers zéro quand n tend vers l'infini.
-
fidelcastro
- Messages: 7
- Enregistré le: 10 Juin 2006, 18:58
-
 par fidelcastro » 11 Juin 2006, 10:45
par fidelcastro » 11 Juin 2006, 10:45
Donc dans le message 10 ne serait ce pas plutot Rn(x) que Vn(x)?
-
mathelot
 par mathelot » 11 Juin 2006, 11:06
par mathelot » 11 Juin 2006, 11:06
oui, tout à fait exact. et de plus, c'est l'intervalle semi-ouvert
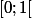
car la somme
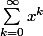
n'est pas définie pour x=1
-
fidelcastro
- Messages: 7
- Enregistré le: 10 Juin 2006, 18:58
-
 par fidelcastro » 11 Juin 2006, 11:18
par fidelcastro » 11 Juin 2006, 11:18
Et comment fait-on pour passer de l'inegalité du message 13 a l 'inegalité du message 10?
-
mathelot
 par mathelot » 11 Juin 2006, 11:29
par mathelot » 11 Juin 2006, 11:29
on minore chaque terme
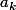
par

à partir du rang
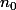
puisque l est la limite de la suite de terme général
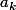
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
