Séries : S(u) et S(v) convergent, quid S(uv) ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nathanap
- Membre Naturel
- Messages: 46
- Enregistré le: 30 Juin 2010, 18:58
-
 par nathanap » 13 Aoû 2010, 17:20
par nathanap » 13 Aoû 2010, 17:20
Bonjour,
Voici un exercice sur les séries qui ne semble pas classé parmi les exercices difficiles de mon cours et que je n'arrive pas à faire (honte à moi) :
On considère deux suites complexes u et v. On suppose que les séries S(u) et S(v) de termes généraux u et v convergent, que dire de la suite de terme général u*v ?
Je n'arrive à une solution que quand les deux suites sont réelles positives ... Alors S(u*v) converge : dans ce cas la suite (S(u)S(v)) est supérieure à S(u*v) pour tout n puisqu'on retrouve les termes de la somme S(u*v) dans le produit S(u)S(v) et comme S(u)S(v) converge et que S(u*v) est croissante c'est bon .. Mais bon c'est pas génial comme résultat ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Aoû 2010, 17:24
par girdav » 13 Aoû 2010, 17:24
On ne peut pas toujours conclure la convergence. Par exemple, avec
^n}{\sqrt n})
les séries de terme général

et

convergent, mais
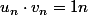
.
-
nathanap
- Membre Naturel
- Messages: 46
- Enregistré le: 30 Juin 2010, 18:58
-
 par nathanap » 13 Aoû 2010, 17:29
par nathanap » 13 Aoû 2010, 17:29
Merci ! En effet j'ai bêtement cru qu'il fallait chercher à prouver qu'elle convergeait au lieu de chercher un contre exemple ...
-
Dihtbscii
- Membre Naturel
- Messages: 40
- Enregistré le: 07 Fév 2010, 18:23
-
 par Dihtbscii » 13 Aoû 2010, 17:41
par Dihtbscii » 13 Aoû 2010, 17:41
Non mais il ne faut pas confondre la suite uv et la série. Pour la suite uv il y a bien un résultat évident; la suite converge vers 0. Pour la série il n'y a rien à dire.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2010, 18:49
par Nightmare » 13 Aoû 2010, 18:49
Salut,
on a convergence de la série produit par exemple lorsque les deux séries sont absolument convergente. Sinon, dans le cas général, on ne peut rien dire, comme le démontre si bien Girdav.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 14 Aoû 2010, 11:59
par girdav » 14 Aoû 2010, 11:59
Cependant, si les séries de terme général
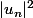
et
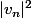
convergent alors par l'inégalité
)
on déduit l'absolue convergence la série de terme général
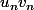
.
Mais ceci est une condition suffisante, et non nécessaire.
-
dibeteriou
- Membre Naturel
- Messages: 91
- Enregistré le: 17 Aoû 2010, 04:06
-
 par dibeteriou » 17 Aoû 2010, 13:48
par dibeteriou » 17 Aoû 2010, 13:48
Bonjour à tous :)
Il suffit en fait de S(u) absolument convergente et v bornée pour avoir la convergence absolue de S(uv).
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Aoû 2010, 16:55
par girdav » 17 Aoû 2010, 16:55
Si la série des

ou celle des

converge absolument alors on peut déduire que la série de terme général
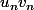
converge absolument (puisque par exemple si
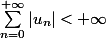
, on a par les hypothèses initiales que
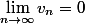
donc la suite
)
est bornée par exemple par

donc
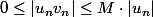
).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
