Série trigonométrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
tartar
- Messages: 4
- Enregistré le: 20 Avr 2008, 08:32
-
 par tartar » 17 Aoû 2010, 20:01
par tartar » 17 Aoû 2010, 20:01
Bonjour à tous !
Voilà je viens à vous pour solliciter votre aide par rapport à un calcul.
Soit la fonction :

Si vous pouviez m'aider à comprendre svp
-
dibeteriou
- Membre Naturel
- Messages: 91
- Enregistré le: 17 Aoû 2010, 04:06
-
 par dibeteriou » 17 Aoû 2010, 20:10
par dibeteriou » 17 Aoû 2010, 20:10
Regarde ce qu'il y a sous ta somme :we:
Normalement, l'indice

varie dans

.
-
tartar
- Messages: 4
- Enregistré le: 20 Avr 2008, 08:32
-
 par tartar » 17 Aoû 2010, 20:24
par tartar » 17 Aoû 2010, 20:24
Ahhhh d'accord ! Oui je le voyais pas comme ça. Donc n varie dans R c'est bien ça ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Aoû 2010, 08:51
par girdav » 18 Aoû 2010, 08:51
Dans la première somme

varie dans

. On a
+b_n\sin (nx) &=\sum_{n=0}^{+\infty}\fr{a_n-ib_n}2e^{inx} +\fr{a_n+ib_n}2e^{-inx}\\<br />&=a_0 +\sum_{n=1}^{+\infty}\fr{a_n-ib_n}2e^{inx} +\sum_{m=1}^{+\infty}\fr{a_m+ib_m}2e^{-imx}\\<br />&=a_0 + \sum_{n=1}^{+\infty}\fr{a_n-ib_n}2e^{inx}+\sum_{n=-\infty}^{-1}\fr{a_{-n}+ib_{-n}}2 e^{inx}<br />\end{align})
.
Il ne reste plus qu'à identifier les termes :

, pour

on a
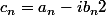
et pour

on a
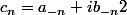
.
-
tartar
- Messages: 4
- Enregistré le: 20 Avr 2008, 08:32
-
 par tartar » 18 Aoû 2010, 20:02
par tartar » 18 Aoû 2010, 20:02
Trés clair comme explication =) merci. Par contre, Co = Ao plutôt nan ? pour n=0, l'expression vaut Ao, à moins que je sois vraiment fatigué ce soir :D
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 18 Aoû 2010, 20:54
par girdav » 18 Aoû 2010, 20:54
Oui merci, entre nous deux, c'est moi le plus fatigué. M'en vais de ce pas corriger ces coquilles.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités

