Série

[nelloune]

Bonsoir,
Je bloque sur la nature de la série de terme général:

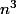
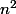
dn=(1+)^1/3-(1+)^1/2

Ma première idée est de faire l'équivalence mais je tombe sur 0

[aviateur]

Bonjour
L'équivalence ça marche pas d'abord parce qu'on ne fait pas de différence avec les équivalents, il faut faire un DL

[penser à mettre n en facteur pour avoir quelque chose de la forme (1+u)^a=(1+a u+o(u)) quand u tend vers 0)]

(1+n^3)^(1/3)=n (1+1/n^3)^(1/3)=n(1+ 1/3 1/n^3+o(1/n^3))=n+1/(3 n^2)+o(1/n^2))
de même
(1+n^2)^(1/2)=n (1+1/n^2)^(1/2)=n(1+ 1/2 1/n^2+o(1/n^2))=n+1/(2 n)+o(1/n))

D'où d_n=1/(2n) +o(1/n)
On peut conclure avec la
série de terme général [1/n] qui est ...

[tournesol]

Bonsoir aviateur
Il me semble que tu as mal développé ta septième ligne .

[nelloune]

D'accord, je vois ce qu'il faut faire merci

[aviateur]

Bonsoir aviateur
Il me semble que tu as mal développé ta septième ligne .

Exact donc j'ai rectifié alors ça change l'équivalent et aussi la nature de la série.
Je pense que @Nelloune aura corrigé l'erreur aussi