Série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
derkaoui
- Messages: 5
- Enregistré le: 16 Oct 2013, 12:13
-
 par derkaoui » 16 Oct 2013, 13:26
par derkaoui » 16 Oct 2013, 13:26
Bonjour,
je veux savoir la nature de la série de terme général
(n+2)...2n}{(2n)^n})
merci d'avance!
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 16 Oct 2013, 13:37
par arnaud32 » 16 Oct 2013, 13:37
derkaoui a écrit:Bonjour,
je veux savoir la nature de la série de terme général
(n+2)...2n}{(2n)^n})
merci d'avance!
ta serie converge
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 16 Oct 2013, 13:38
par Monsieur23 » 16 Oct 2013, 13:38
Aloha,
Réécris le numérateur en fonction de factorielle, puis Stirling.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 16 Oct 2013, 13:56
par deltab » 16 Oct 2013, 13:56
Bonjour
arnaud32 a écrit:ta serie converge
Je ne vois pas pourquoi.
(n+3)\codts (2n-1)2n(2n+1)(2(n+1))\times (2n)^n}{(2(n+1))^{n+1} \times (n+1)(n+2)\cdots (2n-1)(2n))
-
derkaoui
- Messages: 5
- Enregistré le: 16 Oct 2013, 12:13
-
 par derkaoui » 16 Oct 2013, 13:59
par derkaoui » 16 Oct 2013, 13:59
Monsieur23 a écrit:Aloha,
Réécris le numérateur en fonction de factorielle, puis Stirling.
merci pour l'idée :lol3:
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 16 Oct 2013, 14:16
par arnaud32 » 16 Oct 2013, 14:16
plus basique:
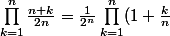)
tu utilises
1/

2/
}{2n})
3/

-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 16 Oct 2013, 14:18
par deltab » 16 Oct 2013, 14:18
Bonjour

se présente sous forme de produits, la règle la plus indiquée à tester en premier lieu est la règle de D'Alembert.
-
derkaoui
- Messages: 5
- Enregistré le: 16 Oct 2013, 12:13
-
 par derkaoui » 16 Oct 2013, 17:07
par derkaoui » 16 Oct 2013, 17:07
Merci bcp!
-
derkaoui
- Messages: 5
- Enregistré le: 16 Oct 2013, 12:13
-
 par derkaoui » 22 Nov 2013, 17:33
par derkaoui » 22 Nov 2013, 17:33
Bonjour!
Je veux étudier la convergence uniforme sur [0;1] de la suite de fonctions :
[CENTER]
 <br /> \alpha \in R.)
[/CENTER]
J'ai bloqué dans le cas
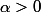
:mur:
-
Elizabet
- Membre Naturel
- Messages: 54
- Enregistré le: 19 Aoû 2013, 15:16
-
 par Elizabet » 22 Nov 2013, 18:33
par Elizabet » 22 Nov 2013, 18:33
derkaoui a écrit:Bonjour!
Je veux étudier la convergence uniforme sur [0;1] de la suite de fonctions :
[CENTER]
 <br /> \alpha \in R.)
[/CENTER]
J'ai bloqué dans le cas
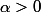
:mur:
Si
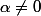
,
étudie les variations de la fonction avec
)
et cherche la limite simple avant celle uniforme par l'équivalent de :

?.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2013, 18:40
par Ben314 » 22 Nov 2013, 18:40
Salut,
Si tu étudie les variations de

sur [0,1] tu va trouver qu'elle est positive et admet un max en

facile à calculer.
Tu évalue ensuite
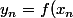)
.
Si

tend vers 0 alors ta suite de fonction converge normalement (donc uniformément) vers 0.
Si

ne tend pas vers 0, mais vers une limite L, il peut être interessant de comparer L avec la limite des
)
où l est la limite des

. Si la limite est différente de L, cela montre que...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 22 Nov 2013, 19:36
par deltab » 22 Nov 2013, 19:36
Bonjour.
On veut calculer
 =\lim_{n \to \infty} n^\alpha x^n (1-x))
pour
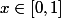
.
=f_n(1)=0)
donc
=\lim_{n \to \infty] f_n(1)=0.)
Pour
)
en tant que fonction de n (on cherche la limite quand
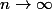
) se présente sous la forme d'un produit de 3 termes, une constante
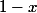
, d'une fonction puissance

et d'une exponentielle (de base x)

, on aura donc
=0)
. La limite simple

sur

est donc la fonction nulle,
=0)
pour
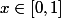
.
-
derkaoui
- Messages: 5
- Enregistré le: 16 Oct 2013, 12:13
-
 par derkaoui » 22 Nov 2013, 20:55
par derkaoui » 22 Nov 2013, 20:55
j'ai trouvé qu'on a la convergence uniforme sur [0,1] si et ssi
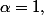
la suite

est uniformément converge sur ]0,1[

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2013, 22:06
par Ben314 » 22 Nov 2013, 22:06
J'ai de gros doutes : la suite

converge simplement vers la fonction nulle
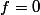
pour tout réel

(plus petit ou plis grand que 1) : voir le post de deltab çi desssus.
Donc le sup de
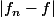
est en fait le sup de

qui est
\sim e^{-1}n^{\alpha-1})
et qui ne tend pas vers 0 si

...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 22 Nov 2013, 23:35
par deltab » 22 Nov 2013, 23:35
Bonsoir
Ben314 a écrit:J'ai de gros doutes : la suite

converge simplement vers la fonction nulle
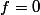
pour tout réel

(plus petit ou plis grand que 1) : voir le post de deltab çi desssus.
Donc le sup de
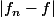
est en fait le sup de

qui est
\sim e^{-1}n^{\alpha-1})
et qui ne tend pas vers 0 si

...
Tu n'as pas à en douter, on n'a pas pas effectivement de convergence uniforme. Je rappelle que
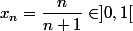
pour
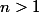
et
=\dfrac{n^{\alpha -1}}{1+1/n}\tex{ }\dfrac{1}{(+1/n)^n})
.
On a donc
-f(x)|=\lim_{n\to +\infty}f_n(x_n)= \left\lbrace\begin{array} 0 \text{ si } \alpha 1 \end{array})
.
On a donc bien la convergence uniforme pour
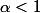
et on on ne l'a pas pour


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2013, 23:44
par Ben314 » 22 Nov 2013, 23:44
Par contre, vu le type d'exo., je pense que le truc un peu intéressant à montrer, c'est que pour tout

fixé, la suite de fonction converge uniformément sur

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 22 Nov 2013, 23:46
par deltab » 22 Nov 2013, 23:46
et on a bien la convergence uniforme pour tout
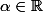
sur l'intervalle [0,b] avec
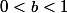
. Ceci provient du fait que
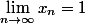
et donc à partir d'un certain

,

n'est plus dans

et à partir de ce rang
-f(x)|=f_n(b))
et
-f(x)|=\lim_{n \to \infty} f_n(b)=0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
converge simplement vers la fonction nulle
pour tout réel
(plus petit ou plis grand que 1) : voir le post de deltab çi desssus.
est en fait le sup de
qui est
et qui ne tend pas vers 0 si
...