Bonsoir, j'ai un bête problème sur des séries, je n'arrive pas à les encadrer par intégrales et pourtant c'est ce qu'il faut faire.
Cn = Re ( i ^(n+1))
On veut calculer S(Cn) = somme (de n=1 à +inf) ( Cn/n )
et il est rappelé que quel que soit K l'intégrale de 0 à 1 de t^k = 1/(k+1)
Pourriez-vous m'éclaircir car je n'arrive pas à obtenir le bon encadrement de départ.
Il me semblait pourtant que pour trouver une somme il était plus simple de trouver des séries télescopiques que de calculer une intégrale non ?
Est-ce que ça veut dire que ici il va y avoir des chances que ça tende vers 0 ?
Série
4 messages
- Page 1 sur 1
Salut. Tu dis que cn est nul pour n pair, et si n=2p+1, cn=(-1)^p+1.
Tu peux donc déjà écrire ta somme différemment, en supprimant les termes pairs.
Ensuite, tu dis que 1/2p+1=integrale de t^2p (cf indication), et en permutant (permutation licite, mais il faut le prouver), tu obtiens ta somme comme l'inttegrale d'une serie géometrique de raison (-t^2), ce que tu sais calculer.
Tu peux donc déjà écrire ta somme différemment, en supprimant les termes pairs.
Ensuite, tu dis que 1/2p+1=integrale de t^2p (cf indication), et en permutant (permutation licite, mais il faut le prouver), tu obtiens ta somme comme l'inttegrale d'une serie géometrique de raison (-t^2), ce que tu sais calculer.
En fait t'as les termes pairs de ta somme qui sont nuls: Re(i^2n+1)=0.
Donc en fait tu obtiens:
Ta somme=^{p+1}}{2p+1}) (verifie les indices, je fais de tête j'ai peut être un peu merdé.
(verifie les indices, je fais de tête j'ai peut être un peu merdé.
Ensuite, tu dis que^{p}}{2p+1}=\int^{1}_{0}(-t^2)^pdt)
Et il faut ensuite que tu justifies que tu peux permuter l'integrale et la somme pour aboutir à
Ta somme=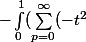^p)dt) , que tu peux calculer.
, que tu peux calculer.
Donc en fait tu obtiens:
Ta somme=
Ensuite, tu dis que
Et il faut ensuite que tu justifies que tu peux permuter l'integrale et la somme pour aboutir à
Ta somme=
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
