Série numérique !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Sep 2007, 18:51
par barbu23 » 01 Sep 2007, 18:51
Bonjour :
J'essaye de trouver la nature de la serie de terme general
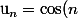 $)
?
D'abord, je calcule :
.dt $)
:
.dt = [sin(t)]_{0}^{+\infty} = \displaystyle \lim_{t \longrightarrow +\infty} \hspace{10cm} \sin(t) $)
... Ensuite la nature de la serie est exactement celle de l'integrale que j'essaye de calculer ( Est ce que c'est la bonne methode ou bien on peut faire plus simple que cette methode ?)
Ma question est :
Qelle est la limite de sin à l'infini :
 $)
Merci d'avance !!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Sep 2007, 18:53
par Nightmare » 01 Sep 2007, 18:53
Oula !
Quand même, on travail pas sur les séries quand on ne sait pas que sin n'a pas de limite en +oo :briques: , il suffit de regarder sa courbe pour s'en convaincre après tout.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Sep 2007, 18:57
par Nightmare » 01 Sep 2007, 18:57
Bref, ta série est clairement divergente, vu que son terme général ne converge pas vers 0.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Sep 2007, 18:57
par barbu23 » 01 Sep 2007, 18:57
D'accord, et comment se resout cet exo ?!
Avec un D.L. au voisinage de l'infini peut-t-on s'en sortir, j'ai pas encore essayé ?!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Sep 2007, 19:00
par Nightmare » 01 Sep 2007, 19:00
Ben il est résolu l'exercice, ta série est divergente.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Sep 2007, 19:01
par barbu23 » 01 Sep 2007, 19:01
ah oui tu as raison, merci, j'ai étudié les series numeriques et integrales generalisées il y'a deux ans, il faut que je recommence à reviser ces cours là, j'ai presque tous oublié !!!
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 01 Sep 2007, 19:04
par quinto » 01 Sep 2007, 19:04
D'autant plus que ce n'est pas parce qu'une intégrale diverge que la série associée diverge aussi et réciproquement ...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 01 Sep 2007, 21:59
par Joker62 » 01 Sep 2007, 21:59
Oui on a besoin de la décroissance et de la positivité de la fonction f pour faire une comparaison entre série et intégrale.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Sep 2007, 22:16
par barbu23 » 01 Sep 2007, 22:16
oui j'ai oublié tous ça !! :marteau:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Sep 2007, 22:42
par barbu23 » 01 Sep 2007, 22:42
Bonsoir :
Soit
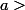
.
Je cherche la limite de l'expression suivante :
^{n} $)
.
voiçi ce que je trouve moi :
^{n} = \displaystyle \lim_{n \longrightarrow +\infty} a^{n} \hspace{10cm} \times \hspace{10cm} \displaystyle \lim_{n \longrightarrow +\infty} \frac{1}{1+(\frac{1}{n})^{n}}= \frac{1}{e} \hspace{10cm} \times \hspace{10cm} \displaystyle \lim_{n \longrightarrow +\infty} a^{n} $)
.
car :
^{n} = e $)
, n'est ce pas ?!
( et pour terminer, on fait l'étude de la suite selon les valeurs de "a" )
Dans le corrigé du bouquin ou j'ai trouvé cet exo, on raisonne de la manière suivante :
^{n} = (\frac{a}{1+\frac{1}{n}})^{n} \longrightarrow a^{n} $)
car :
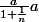
quant
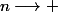
Alors, je suis un peu confus là, qu'est ce qui va pas dans mon raisonnement, pouvez vous m'indiquer où est l'erreur ?!!
Merci d'avance !!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Sep 2007, 22:46
par Nightmare » 01 Sep 2007, 22:46
L'expression ne peut pas tendre vers a^n qui dépend encore de n...
Ce que tu as fait est juste.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Sep 2007, 00:11
par barbu23 » 03 Sep 2007, 00:11
Bonsoir :
Est ce que si une une suite
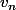
est "croissante" ( et non pas "decroissante" comme c'est le cas du critère de Leibnitz ) et tend vers

alors la serie de terme general
.v_{n} $)
converge ?
Dans certains cours, on enonce le critère de Leibnitz comme suit :
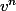
est decroissante et tend vers

alors : la serie de terme general
.v_{n} $)
converge .. Dans d'autres cours :la serie de terme general
.v_{n} $)
converge si
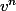
est "monotone" et tend vers

.
Lesquels de ces cours ont parfaitement raison ?!
Merci d'avance !!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 03 Sep 2007, 00:20
par fahr451 » 03 Sep 2007, 00:20
bonsoir
si v n est croissante de limite nulle
un = -vn est décroissante de limite nulle
la série de terme général wn = (-1)^n vn converge ssi la série de terme général -wn = (-1)^n u n converge
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Sep 2007, 00:22
par Nightmare » 03 Sep 2007, 00:22
Salut, il y a critère de Leibniz et critère d'Abel... Le critère de Leibniz s'applique pour une suite décroissante, le critère d'Abel pour une suite monotone.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Sep 2007, 01:31
par barbu23 » 03 Sep 2007, 01:31
Bonsoir :
Merci beaucoup pour ces precisions "Nightmare" et "fahr451" :
J'ai une autre question à vous poser :
Combien vaut :
^{n}}{n} $)
?
Mon problème est que je crainds qu'il n'ait pas de limite puisque c'est une suite alternée, elle ressemble un peu à celle çi :
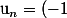^{n} $)
et
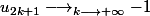
et
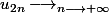
,donc la limite n'existe pas ), je peux facilement dire qu'elle vaut

, mais elle manque d'arguments ... Bref,
^{n}}{n} - 0 \| \leq \frac{1}{n} \displaystyle \longrightarrow_{n \longrightarrow +\infty} 0 $)
donc :
^{n}}{n} = 0 $)
... Est ce qu'il est correct ce raisonnement ?!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Sep 2007, 01:44
par barbu23 » 03 Sep 2007, 01:44
Je pense que c'est correct .. !
C'est trop stupide ce que je raconte ... :ptdr:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Sep 2007, 02:22
par Nightmare » 03 Sep 2007, 02:22
Oui en effet ta suite est majorée en valeur absolue par 1/n donc converge vers 0.
Autre raisonnement : Les deux suites extraites (U2n) et (U2n+1) convergent vers 0 donc il en va de même pour (Un)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Sep 2007, 21:44
par barbu23 » 03 Sep 2007, 21:44
Bonsoir:
Je cherche à établir que la serie de terme général
^{n}.n}{n^{2}+1} = (-1)^{n}.v_{n} $)
converge avec :
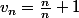
.
On a :
1)
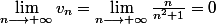
.
2)
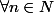
:
^{2}+1} - \frac{n}{n^{2}+1} = ... = - \frac{n^{2}+n-1}{(n^{2}+1)((n+1)^{2}+1)} $)
.
Maintenant, on étudie le signe de :
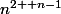
.
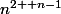
admet deux solutions :
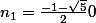
, ( mais pour
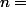
, c'est pas le cas )
Donc :
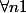
:
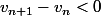
... Donc,
_{n \in \mathbb{N}} $)
est décroissante sur :
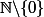
...
Peut-on conclure, maintenant, que la serie de terme general
^{n}.n}{n^{2}+1} = (-1)^{n}.v_{n} $)
converge, même si la décroissance n'est pas verifier sur tout
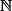
, mais uniquement sur :
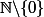
( il manque

pour établir le critère de Leibnitz ou Abel ).
Merci d'avance !!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Sep 2007, 21:49
par Nightmare » 03 Sep 2007, 21:49
Salut,
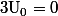
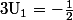
Donc
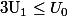
La suite est bien décroissante sur N.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Sep 2007, 22:02
par barbu23 » 03 Sep 2007, 22:02
Merci pour la reponse .. !
Et si jamais on tombe sur une suite qui est décroissante sur
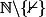
mais pas sur
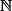
, alors est ce qu'on peut dans ce cas appliquer le critère de Leibnitz ou d'Abel ?!
Merci d'avance !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités