Série numérique !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 18:13
par fahr451 » 04 Sep 2007, 18:13
bonsoir
la première preuve peut se faire en TS
pas la seconde
 par sandrine_guillerme » 04 Sep 2007, 18:17
par sandrine_guillerme » 04 Sep 2007, 18:17
Bonsoir fahr
il me semble que barbu23 est en L3 ..
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Sep 2007, 18:33
par barbu23 » 04 Sep 2007, 18:33
oui exact !! :lol2:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 19:05
par fahr451 » 04 Sep 2007, 19:05
ah alors c 'est un savant
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Sep 2007, 19:54
par barbu23 » 04 Sep 2007, 19:54
Bonjour:
Soit
 $)
.
Soit

.
Alors :
 .dt = 0 $)
.
je cherche la demonstration de ce Lemme appelé Lemme de Lebesgue !
Merci d'avance !!
P.S : J'ai dejà une demonstration de ce lemme dans un livre, mais j'arrive pas encore à la comprendre !
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 19:56
par fahr451 » 04 Sep 2007, 19:56
bonsoir IPP
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Sep 2007, 20:26
par barbu23 » 04 Sep 2007, 20:26
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 20:41
par fahr451 » 04 Sep 2007, 20:41
maintenant sans les mains :
le même résultat pour f intégrable
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Sep 2007, 23:33
par barbu23 » 04 Sep 2007, 23:33
D'accord !!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Sep 2007, 01:08
par barbu23 » 05 Sep 2007, 01:08
Bonsoir :
Voiçi une autre serie un peu compliqué :
Question :
Etudier la serie de termes general :
}{Arctan(n+1)})^{n^{3}} $)
Voiçi comment je procède :
}{Arctan(n+1)})^{n^{3}} = e^{n^{3}. (\ln(Arctan(n))-\ln(Arctan(n+1))) $)
On a : au voisinage de

à l'ordre de

:
 = x-\frac{x^{3}}{3}+\frac{x^{5}}{5}-...+(-1)^{n}.\frac{x^{2.n+1}}{2.n+1}+o(x^{2.n+2}) $)
.
Alors, à partir d'ici, je sais plus quoi faire, car
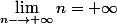
et la formule du D.L. qu'on a ci-dessus est defini au voisinage de

et non pas de
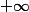
.
Quelqu'un peut m'aider pour la suite ?!
Merci d'avance de votre aide !!
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 05 Sep 2007, 01:21
par Sylar » 05 Sep 2007, 01:21
Bonsoir,peut-être on peut essayer de calculer:
lim(n->+inf) [u_(n+1)] / u_n
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Sep 2007, 01:33
par barbu23 » 05 Sep 2007, 01:33
Est ce que c'est valable avec la formule suivante :
 = \frac{\pi}{2} - Arctan(\frac{1}{x}) $)
?
Donc, ça va devenir comme ça :
}{\frac{\pi}{2}-Arctan(\frac{1}{n+1})})} = e^{n^{3}.\ln(\frac{1-\frac{2}{\pi}.Arctan(\frac{1}{n})}{1-\frac{2}{\pi}.Arctan(\frac{1}{n+1})})} = e^{n^{3}.(\ln(1-\frac{2}{\pi}.Arctan(\frac{1}{n}) - \ln(1-\frac{2}{\pi}.Arctan(\frac{1}{n+1}))) $)
Et là :
 \displaystyle \longrightarrow_{n \longrightarrow +\infty} 0 $)
et
 \displaystyle \longrightarrow_{n \longrightarrow +\infty} 0 $)
Alors, ça va comme ça ...?? est ce que je suis sur la bonne voix... ?!
Merci d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Sep 2007, 01:33
par barbu23 » 05 Sep 2007, 01:33
oui Sylar, je vais essayer !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Sep 2007, 01:37
par barbu23 » 05 Sep 2007, 01:37
oui mais ça donne une formule trop compliquée, je ne crois pas que ça va aboutir à quelque chose d'utile avec ce critère d'Alembert que tu proposes !!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Sep 2007, 08:29
par fahr451 » 05 Sep 2007, 08:29
bonjour
oui tu es sur la bonne voiE
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Sep 2007, 21:57
par barbu23 » 05 Sep 2007, 21:57
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Sep 2007, 22:02
par fahr451 » 05 Sep 2007, 22:02
bonsoir
ta maladresse vient du fait que tu ne fais pas IMMEDIATEMENT le dv de
1/(n+1) = 1/[n(1+1/n)] = ...
 par legeniedesalpages » 05 Sep 2007, 23:40
par legeniedesalpages » 05 Sep 2007, 23:40
Ca c'est vraiment barbu! (désolé je n'ai pas pu m'empêcher :lol2:, veuillez m'excuser pour cette impédance!)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Sep 2007, 23:14
par barbu23 » 06 Sep 2007, 23:14
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 07 Sep 2007, 14:14
par fahr451 » 07 Sep 2007, 14:14
c'était rapide finalement :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
}{Arctan(n+1)})^{n^{3}} $)
}{Arctan(n+1)})^{n^{3}} = e^{n^{3}. (\ln(Arctan(n))-\ln(Arctan(n+1))) $)
 à l'ordre de
à l'ordre de  :
: = x-\frac{x^{3}}{3}+\frac{x^{5}}{5}-...+(-1)^{n}.\frac{x^{2.n+1}}{2.n+1}+o(x^{2.n+2}) $) .
.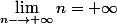 et la formule du D.L. qu'on a ci-dessus est defini au voisinage de
et la formule du D.L. qu'on a ci-dessus est defini au voisinage de  et non pas de
et non pas de 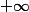 .
., on peut pas simplifier cette dernière expression ...?
