Série Harmonique alternée généralisée

[Aspx]

Bonjour !

J'ai récemment fait quelques petites recherches sur les séries harmoniques et j'ai trouvé la formule suivante, donnant la valeur d'une série alternée harmonique (une variante de l'initiale) :

[CENTER][/CENTER]

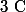
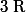
Je me demandais donc si, pouron pouvait exprimer cette valeur de manière générique. J'ai donc décomposé la fraction rationnellesuravec une variante des racines n-ièmes de l'unité. Je me demandais si il n'était pas judicieux de décomposer la fraction suravec les dénominateurs de degré 2.

Ma décomposition est :
[CENTER][/CENTER]
avecles racines n-ièmes de l'unité et

(le véritable polynôme s'obtient en effectuant le changement)

Merci bien !

[Aspx]

En gros ma question est la suivante : est-ce que l'extension du logarithme au disque unité privé de -1 peut servir à réduire l'intégration ou est-on obligé d'utiliser les facteurs de degré 2 (arctan & co).

[Joker62]

Le théorème des résidus sur un secteur contenant un seul pôle de l'intégrande est quand même plus pratique est donne un joli résultat si je m'en rapelle bien.

[Aspx]

Ça à l'air alléchant comme résultat mais l'analyse complexe n'est pas au programme de spé ! :cry: Une autre idée ?

[mathelot]

bonsoir,

j'aurais écrit:



et regardé les racines nième de -1 et non de 1.

[Aspx]

Oui c'est que j'ai précisé (un changement de variable permet de s'y ramener)