Série et fractions rationelles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 16 Juin 2008, 17:50
par fenecman » 16 Juin 2008, 17:50
Bonsoir,
Voici l'exercice proposé :
Soit P et Q deux polynômes n'ayant aucun entier naturel comme racine.étudier la nature de la série
}{Q(n)}|)
.
J'ai tout d'abors montré que pour que la série ne diverge pas grossièrement il fallait que P et Q aient le meme degré et le même coéfficient dominant.
Ensuite j'ai voulu montrer que si les racines de P n'étaient pas celles de Q alors la série diverge.
Mais pour cela j'ai utiliser le résultats :
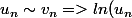 \sim ln(v_n))
( en prenant les suite dans R+* )
Mais je m'intérogeait sur la validité de ce résultat...
Merci de votre aide
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 16 Juin 2008, 18:38
par kazeriahm » 16 Juin 2008, 18:38
Salut,
le fait qu'ils aient les mêmes racines ne fait que réduire le problème, tu vas te retrouver avec du P'(n)/Q'(n) avec P' et Q' de même degré et de même coefficient dominant
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 16 Juin 2008, 20:19
par fenecman » 16 Juin 2008, 20:19
Mais si ils ont les mêmes racines et le même coefficient dominant alors P(n)/Q(n) = 1 .
Je comprends pas très bien ce ke tu veu dire ...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Juin 2008, 20:46
par yos » 16 Juin 2008, 20:46
Ecris
}{Q(n)}=1+\frac{P(n)-Q(n)}{Q(n)})
et donne un équivalent du logarithme.
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 17 Juin 2008, 07:51
par fenecman » 17 Juin 2008, 07:51
D'accord donc en prenant le module et en passant aux logarithmes, j'obtient que si le coefficient de X^(k-1) est le même dans les deux polynomes alors U_n est équivalente à 1/n^2 d'où convergente.?
Mais si les coefficients de X^(k-1) ne sont pas les mêmes?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 17 Juin 2008, 16:01
par yos » 17 Juin 2008, 16:01
Il faut évacuer le module en disant que P(n)/Q(n) garde un signe constant pour n>N.
Si les coefs de X^{k-1} de P et Q coïncident, c'est plutôt du O(1/n^2) (ça peut être a/n^2 ou a/n^3 ...).
Dans l'autre cas c'est équivalent à du a/n.
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 17 Juin 2008, 17:56
par fenecman » 17 Juin 2008, 17:56
yos a écrit:Il faut évacuer le module en disant que P(n)/Q(n) garde un signe constant pour n>N.
Salut,
Je comprends pas comment tu peux enlever le module si P et Q ont des coefficients complexes?
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 17 Juin 2008, 19:59
par Lierre Aeripz » 17 Juin 2008, 19:59
fenecman a écrit: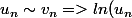 \sim ln(v_n))
C'est faux !
Exemple :
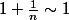
, mais
 \not\sim 0)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 17 Juin 2008, 20:34
par yos » 17 Juin 2008, 20:34
fenecman a écrit:Je comprends pas comment tu peux enlever le module si P et Q ont des coefficients complexes?
Je les voyais réels.
En ce cas écrit
}{Q(n)}|=\ln(1+r_n))
où
}{Q(n)}|-1)
et fait un dl à l'ordre 2 du log pour contourner la difficulté soulevée par Lierre aerpiz.
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 18 Juin 2008, 14:49
par fenecman » 18 Juin 2008, 14:49
Salut,
Je suis en train de me perdre dans les modules... :marteau:
Est-ce que ça serait possible de préciser un peu plus ??
merci
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 18 Juin 2008, 20:58
par yos » 18 Juin 2008, 20:58
Essaie de garder des égalités :
}{Q(n)}|=1+\frac{a}{n}+O(\frac1{n^2}))
D'autre part
}{Q(n)}|-1|\leq |\frac{P(n)}{Q(n)}-1|)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
