Babe a écrit:a ok et que signifie caractere hilbertien de la base ?
En algèbre linéaire, une base est une famille libre et génératrice. Génératrice signifie que tout vecteur de l'EV s'écrit comme combinaison linéaire
finie d'éléments de la famille (dimension finie ou infinie).
Là, ta famille des cos et sin est libre (c'est une conséquence de l'orthogonalité), mais en général, une fonction de L2(I) n'est une combinaison linéaire
finie d'éléments de la famille. Il faut faire une somme
infinie, une série quoi ! Là, on quitte l'algèbre linéaire classique pour entrer dans le monde hilbertien... tein tein tein...
Du coup, rien ne dit que ta famille est génératrice au sens "hilbertien" (avec une série). En fait, en général, on n'a pas l'égalité
 = sa\ serie\ de\ Fourier (x))
pour tous les
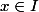
. Il y a des théorèmes qui traitent du problème : par exemple, si f est continue, c'est ok. etc.
