Bonsoir à vous tous.
Je vous propose le problème suivant.
Soit la fonction f(t) = t avec t compris entre-2 et 2, ayant une période T=4s.
1. Calculer la fréquence V0 et la pulsation w0 dre la fonction
2. Tracer la courbe sur l'intervalle -2T et 2T
3. Cette fonction est elle paire impaire.
4. Que pouvons déduire de la valeur des coefficients an et bn
5. A l'aide d'intégration par partie calduler bn
6. Tracer le spectre d'amplitude pour n<6 en donnant les fréquence de chaque raie.
7. Donnez le développement de f(t) de fourier pour n<6
Je trouve.
1. V0= 1/4=0 25 Hz
W0= 2pi/4 =1.57 rad/s
2.
Je trace la courbe sur l'intervalle [-2T, 2T] qui revient à [-8,8].
J'obtiens un droite passant par l'origine.
Qui se répète.
3.
La fonction est impaire car f(x) =-f(x)
4. On peut deviner que an=0 et BN = 4/T intégrale de 0 à 4 f(t) sin (nwt) dt.
Calcul de w = 2.pi/4=pi/2
Après l'intégration par partie je trouve
=(- 4(2cos(2pi.n)-2sin(2pi.n))/n.pi
6. B1=-2.6
B2=-1.31
B3=-0.87
B4=-0.64
B5=-0.50
B6=-0.40
7. F(t) = - 2.6 sin (wt) - 1.31sin(2wt)...-0.40sin(6wt).
Merci...
Serie de fourier
10 messages
- Page 1 sur 1
Re: Serie de fourier
Bonjour tout le monde.
Est ce si faux que ça + ??
Espérant que vous allez bien.
Cordialement
Est ce si faux que ça + ??
Espérant que vous allez bien.
Cordialement
Re: Serie de fourier
Lors du calcul de B1, normalement tu devrais intégrer quelquechose de positif, donc je suis perplexe devant ton résultat négatif.
Sinon, ça vaut combien sin(2pin) et cos(2pin) ?
Sinon, ça vaut combien sin(2pin) et cos(2pin) ?
Re: Serie de fourier
Bonjour
De plus on porra utiliser ceci :
=0) pourn entier
pourn entier
=) 1 si n est pair et -1 si n est impair
1 si n est pair et -1 si n est impair
donc=(-1)^n)
Krampish a écrit:2.
Je trace la courbe sur l'intervalle [-2T, 2T] qui revient à [-8,8].
J'obtiens un droite passant par l'origine. segment de droite
Qui se répète.
3.
La fonction est impaire car f(x) =-f(x)
4. On peut deviner que an=0 oui
et BN = 4/T intégrale de 0 à 4 f(t) sin (nwt) dt. erreur c'est 2/T devant l'intégrale et pour les bornes de l'intégrale il vaut mieux utiliser -2 et 2 car f(t) n'est pas égale à t sur[2;4]
Calcul de w = 2.pi/4=pi/2 oui
Après l'intégration par partie je trouve
=(- 4(2cos(2pi.n)-2sin(2pi.n))/n.pi à rectifier en tenant compte des remarques précédentes
De plus on porra utiliser ceci :
donc
Re: Serie de fourier
Bonjour
Tout d'abord merci pour ton aide.
Après les remarques je trouve que
Bn=-4cos(n.pi)-4cos(-n.pi)(n.pi) / 2(npi)^2
Mais j'ai un gros doute
Tout d'abord merci pour ton aide.
Après les remarques je trouve que
Bn=-4cos(n.pi)-4cos(-n.pi)(n.pi) / 2(npi)^2
Mais j'ai un gros doute
Re: Serie de fourier
Bonjour
Cela ressemble mais il doit y avoir une erreur...
voyons les résultats intermédiaires
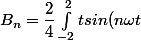dt}=\dfrac{1}{2}\int_{-2}^{2}{tsin (n \omega t)dt})
Posons
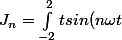dt})
Soit=t) et v'(t)=
et v'(t)=)
donc=1) et v(t)=
et v(t)=)
d'où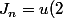v(2)-u(-2)v(-2)-\dfrac{-1}{n \omega}\int_{-2}^{2}cos (n \omega t)dt})
D'accord jusque là ?
La dernière intégraledt}) est en fait égale à zéro.
est en fait égale à zéro.
Cela ressemble mais il doit y avoir une erreur...
voyons les résultats intermédiaires
Posons
Soit
donc
d'où
D'accord jusque là ?
La dernière intégrale
Re: Serie de fourier
Je vais écrire comment j'ai fait.
Je ne trouve pas mon erreur.
Bn=1/2 intégrale entre-2 et 2 t.sin(n.pi.t/2)dt
Poir l'intégration par partie je pose.
V'=1
V= t
U'=sin(npit)
U=-2/npi.cos(npit/2)
=[uv] - intégrale u'. v
=[-2/n.pi cos(npi.t/2)*t] - intégrale -2/npi.cos(npit/2)
=[-2/n.pi cos(npi.t/2)*t] + 2/n.pi [2/n.pi.sin(n.pi.t/2)]
= - 4/n.pi(cos(n.pi)+cos(-n.pi) + 2/n.pi (2/n.pi.sin(n.pi)-2/n.pi.sin(-n.pi)
=-4/n.pi(cos(n.pi)+cos(-n.pi) + 2/n.pi +(4sin(npi)-4sin(-n.pi)/(n.pi)^2
Je multiple par 1/2
=(-4/n.pi. cos(n.pi)+cos(-n.pi) + 2/n.pi +4sin(n.pi)-4sin(-n.pi))/((n.pi)^2) *1/2
Je ne trouve pas mon erreur.
Bn=1/2 intégrale entre-2 et 2 t.sin(n.pi.t/2)dt
Poir l'intégration par partie je pose.
V'=1
V= t
U'=sin(npit)
U=-2/npi.cos(npit/2)
=[uv] - intégrale u'. v
=[-2/n.pi cos(npi.t/2)*t] - intégrale -2/npi.cos(npit/2)
=[-2/n.pi cos(npi.t/2)*t] + 2/n.pi [2/n.pi.sin(n.pi.t/2)]
= - 4/n.pi(cos(n.pi)+cos(-n.pi) + 2/n.pi (2/n.pi.sin(n.pi)-2/n.pi.sin(-n.pi)
=-4/n.pi(cos(n.pi)+cos(-n.pi) + 2/n.pi +(4sin(npi)-4sin(-n.pi)/(n.pi)^2
Je multiple par 1/2
=(-4/n.pi. cos(n.pi)+cos(-n.pi) + 2/n.pi +4sin(n.pi)-4sin(-n.pi))/((n.pi)^2) *1/2
Re: Serie de fourier
Krampish a écrit:Je vais écrire comment j'ai fait.
=[uv] - intégrale u'. v
=[-2/n.pi cos(npi.t/2)*t] - intégrale -2/npi.cos(npit/2)
=[-2/n.pi cos(npi.t/2)*t] + 2/n.pi [2/n.pi.sin(n.pi.t/2)]
= - 4/n.pi(cos(n.pi)+cos(-n.pi) + 2/n.pi (2/n.pi.sin(n.pi)-2/n.pi.sin(-n.pi) Ok jusque là même s'il manque parfois des parenthèses...
Mais ensuite il faut se débarrasser de
De plus
à terminer...
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
