bjr a tous, j'ai une question qui me tracasse concernant la parite de certaine fonction. est ce que si une fonction admet sur un intervalle un axe de symetrie , on peut calculer ses coefficients de fourier en admettent bn=0? je pose cette question car dans un exercice que j'ai traite on a donne une fonction f(x)= (x-pi)^2 avec x appartenant [0, 2pi[ il fallait calculer les coefficients de fourier et dans la correction ils ont considere cette fonction comme etant paire sur cet intervalle. svp j'aurai besoin de votre avis a ce sujet.
merci d'avance
Serie de fourier
9 messages
- Page 1 sur 1
Re: serie de fourier
Bonjour
On doit deviner que ta fonction f est périodique (sinon ????).
périodique (sinon ????).
Si c'est le cas, elle est paire. Donc les coefficients " " sont bien nuls.
" sont bien nuls.
On doit deviner que ta fonction f est
Si c'est le cas, elle est paire. Donc les coefficients "
Re: serie de fourier
quel est donc la definition d'une fonction paire puisque le l'axe de symetrie n'est pas en 0
Re: serie de fourier
concernant cette fonction, cette condition n'est pas verifie sauf si je verifie mal
Re: serie de fourier
Pour montrer que  est nul , il suffit de montrer la parité sur
est nul , il suffit de montrer la parité sur 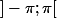 car b_n est le résultat d'une integrale sur
car b_n est le résultat d'une integrale sur 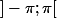 .
.
On a sur cet intervalle ,=f(x+\pi)) (1)
(1)
Soit x dans
on a=f(-x+\pi+\pi)) par
par  periodicite .
periodicite .
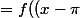+\pi)) par (1)
par (1)
=f(x) .
On a sur cet intervalle ,
Soit x dans
on a
=f(x) .
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
