Serie de Fourier difficile à généraliser

[romzzy]

Bonjour à tous!

Je viens à vous demander de l'aide sur une série de Fourier qui me triture le cerveau depuis hier...

Tout commence avec une fonction peu difficile :

f(x) = 1 si 0<=x<=PI/2
f(x) = 0 si PI/2
Je vais donc travailler sur une intégrale allant de 0 à PI/2 , pour l'instant pas de soucis.

Je trouve donc trois coefficients : a0 = (1/4) ; an = (sin(PI.n/2)) / (PI.n) ; bn = (1-cos(PI.n/2)) / (PI.n) .

Or, mon souci est le suivant : Etant donné que n.PI/2 va prendre 3 valeurs différentes, étant 0, -1 et 1, selon n et sin ou cos, je ne sais comment généraliser l'écriture de ma série... J'ai eu beau chercher sur internet, mais je n'ai pas su trouver d'exemples similaires au mien...

Dans l'attente d'une réponse de votre part, je vous remercie d'avance pour la considération que vous pourriez m'apporter :lol3:

Cordialement,
Romain,
Etudiant en L2 Sciences de l'Information, de l'Audiovisuel et Médias Numériques

[ev85]

Bonjour à tous!

Je viens à vous demander de l'aide sur une série de Fourier qui me triture le cerveau depuis hier...

Tout commence avec une fonction peu difficile :

f(x) = 1 si 0<=x<=PI/2
f(x) = 0 si PI/2<x<2PI

Je vais donc travailler sur une intégrale allant de 0 à PI/2 , pour l'instant pas de soucis.

Je trouve donc trois coefficients : a0 = (1/4) ; an = (sin(PI.n/2)) / (PI.n) ; bn = (1-cos(PI.n/2)) / (PI.n) .

Or, mon souci est le suivant : Etant donné que n.PI/2 va prendre 3 valeurs différentes, étant 0, -1 et 1, selon n et sin ou cos, je ne sais comment généraliser l'écriture de ma série... J'ai eu beau chercher sur internet, mais je n'ai pas su trouver d'exemples similaires au mien...

Dans l'attente d'une réponse de votre part, je vous remercie d'avance pour la considération que vous pourriez m'apporter :lol3:

Cordialement,
Romain,
Etudiant en L2 Sciences de l'Information, de l'Audiovisuel et Médias Numériques

Bonsoir Romain.

Tu vas couper tes sommes partielles en quatre :

quitte par la suite, pour éviter des divergences toujours désagréables, à regrouper des termes non nuls.

[alm]

je ne sais comment généraliser l'écriture de ma série...

Si les expressions ci-dessus sont justes ça suffit en principe.
Je comprends que tu veux finaliser tes calculs.
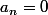
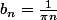
Pour , on remrque que si est paire non nul alors et si est impair alors et pour même principe: si est impaire ça donne et si est pair :

[romzzy]

Un grand merci! :D

Je vais de ce pas, essayer de cette méthode.

Javais rejeté un coup d'oeil dessus, et je m'étais dit qu'enfait, en faisant deux cas : l'un où n=2k , l'autre où n=2k+1 , on remarquait que des parties de la somme se supprimaient en fonction de l'écriture de n.
Je me retrouvais avec quelque chose de correct à la fin, sans savoir pour autant si ma méthode était bonne.

Bref,
Merci de coup de main =)

[romzzy]

Merci MOHAMED_AIT_LH , c'est ce que j'ai fait au final =) .

Je pense que c'est sans faute, surtout si tu m'appuies, mais je vais aussi essayer la méthode de ev85 , ne serait-ce que par curiosité.

Encore merci à vous! :)
Romain

[alm]

Merci de coup de main =)

Je t'en prie et sache que si tes expressions initiales sont exactes alors tu as fait l'esentiel: le reste c'est juste une finition qui d'ailleurs sera gudée par d'éventuelles quetsions qui vienderont après et qui te demanderont de démontrer des formules en utilisant Parseval ou Dirichlet.


PS; j'allais te répondre hier mais j'étais dominé par le sommeil ...

[alm]

ev85

Je n'ai pas bien compris ce que voulais dire ev85 :
D'une part il a utilise la notation : c'est quoi ?
D'autre part : il a partagé la somme en 4 classes : or on a besoin de deux classes seulement : pair et impair...