Série de fonction convergence uniforme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 14:21
salut à tous
je sollicite votre aide à propos d'un exercice, j'ai vraiment séché là-dessus :/
soit la fonction de la variable réelle
 = \sum_{n=1}^{+\infty}\frac{a_n}{n^s})
_{n\in N})
est une suite complexe
On pose pour
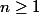
(a) vérifier pour toute suite complexe
_{n\in N})
l'égalité
)
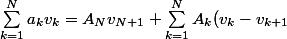(b) on suppose qu'il existe c>0 tel que
et on pose
=]s_0,+\infty[)
montrer que
)
est bien définie sur
)
et que pour tout
)
, la convergence est uniforme sur
j'ai arrivé à faire (a) et la première moitié de (b) mais pour la convergence uniforme j'arrive pas
quelqu'un pourrait m'aider ? merci beaucoup d'avance
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
par aymanemaysae » 22 Nov 2015, 15:56
La question (a) se résout par récurrence :
1) Pour N=1, on Sigma{k=1 à k=N=1}(ak vk) = a1 v1
et AN vN+1 + Sigma{k=1 à k=N=1}(AK(vk- vk+1) = a1 v2+ A1(v1 - v2) = a1 v2+ a1(v1 - v2) = a1 v1,
donc on a: Sigma{k=1 à k=N=1}(ak vk) = AN vN+1 + Sigma{k=1 à k=N=1}(AK(vk- vk+1) .
2) Supposons que pour tout n appartenant à IN* nous avons :
Sigma{k=1 à k=N}(ak vk) = AN vN+1 + Sigma{k=1 à k=N}(AK(vk- vk+1), et essayons de trouver que
Sigma{k=1 à k=N+1}(ak vk) = AN+1 vN+2 + Sigma{k=1 à k=N+1}(AK(vk- vk+1):
AN+1 vN+2 + Sigma{k=1 à k=N+1}(AK(vk- vk+1)
= AN+1 vN+2 + Sigma{k=1 à k=N}(AK(vk- vk+1) + AN+1(vN+1 - vN+2)
= Sigma{k=1 à k=N}(AK(vk- vk+1) + AN+1 vN+1
= Sigma{k=1 à k=N+1}(ak vk) - AN vN+1 + AN+1 vN+1
= Sigma{k=1 à k=N+1}(ak vk) + (AN - AN+1) vN+1
= Sigma{k=1 à k=N+1}(ak vk) + aN+1 vN+1
= Sigma{k=1 à k=N+1}(ak vk)
Donc pour tout N appartenant à IN* on a :
Sigma{k=1 à k=N}(ak vk) = AN vN+1 + Sigma{k=1 à k=N}(AK(vk- vk+1).
Je crois que vous avez trouvé la même chose.
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 17:07
merci mais j'ai besoin de la question (b) , quelqu'un peut m'aider :/ ?
le (a) se fait sans recurence en écrivant
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 19:30
est-ce si difficile :/ ?
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 22 Nov 2015, 19:49
comment as tu fais la convergence simple? Quand je le fais et que je veux passer a a la convergence uniforme j'ai juste à remplacer
par
, ce qui me donne une majoration uniforme
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 20:24
pouvez vous mieux expliquer ? pour la convergence simple j'ai travaillé avec une équivalence,
ps: s n'est pas forcèment positif
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 22 Nov 2015, 20:41
Pour avoir la convergence uniforme tu dois regarder
=\sum_{n=N+1}^ {+\infty}\frac{a_n}{n^s})
.
Ru veux montrer que
tend uniformément vers 0 sur [s1,infini[.
En refaisant une transformée d'abel tu reviens à ca:
=\frac{A_{N}}{(N+1)^{s}}+\sum_{n=N+1}^ {+\infty}A_{n}(\frac{1}{n^{s}}-\frac{1}{(n+1)^{s}}))
Je me place dans le cas s0>0 pour conserver
^{s}}>0)
alors si s1>s0, pour tout
,
 \mid \leq \mid \frac{A_{N}}{(N+1)^{s}} \mid +\sum_{n=N+1}^ {+\infty}\mid A_{n}\mid(\frac{1}{n^{s}}-\frac{1}{(n+1)^{s}}))
En majorant
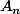
par
. tu fais apparaitre du s0-s, ,et en faisant
t'as une majoration uniforme qui tend vers 0. J'arrete d'écrire les maths ca me suffit la...
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 21:34
jusqu'à cela je suis totalement d'accord avec vous, le premier terme tend uniformément vers 0 ,mais le deuxième est une suite qui tend vers 0 mais dépend de s , comment va-t-on majorer cette suite ?
^s}) \le c \sum_{N+1}^{+\infty}n^{s_0}(\frac{1}{n^s}-\frac{1}{(n+1)^s}))
?
on doit éliminer le s
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 22 Nov 2015, 21:38
MouLou a écrit:En majorant
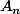
par
. tu fais apparaitre du s0-s, ,et en faisant
t'as une majoration uniforme qui tend vers 0
.
Voila comment t'élimines le s, et apres c le terme d'une serie convergente donc pas ca tend bien vers 0
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 22:03
^s}) \le \frac{1}{n^{s_1-s_0}} - \frac{n^{s_0}}{(n+1)^s})
^s} \ge \frac{1}{(n+1)^{s_1-s_0}})
?
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 22 Nov 2015, 22:25
En fait t'as meme pas besoin de t'emmerder, tu peux te contenter d'écrire:
^s}) \le c (\sum_{N+1}^{+\infty}\frac{n^{s_0}}{n^s}+\sum_{N+1}^{+\infty}\frac{n^{s_0}}{(n+1)^s}))
pour la premiere somme c bon, pour la 2e tu majores
par
^{s_0})
(ca c'est dans le cas s0>0)
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 22:34
mais comment peut on écrire ces restes alors qu'on n'a pas la condition fondamentale s-s0 > 1
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 22 Nov 2015, 22:45
merde t'as raison je raisonnais sur <0... je reflechis
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 22 Nov 2015, 22:57
d'accord ..
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
par Matt_01 » 23 Nov 2015, 00:45
Il faut regrouper le terme 1/n^s -1/(n+1)^s et non les séparer, pour s'apercevoir qu'il est de l'ordre de 1/n^(s+1), ainsi on a à peu près un reste d'une série de Riemann qui converge vers 0 car s1+1 -s0 > 1
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 23 Nov 2015, 00:54
oui exact, merci Matt:
^s})=n^{s}\frac{(1+\frac{1}{n})^{s}-1}{n^{s}(n+1)^{s}}=n^{s}\frac{\frac{s}{n}+o(1/n)}{n^{s}(n+1)^{s}})
qui se comporte comme un terme d'ordre s+1
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 23 Nov 2015, 02:10
c'est une bonne approche
comme vous avez dit :
^s})=n^{s}\frac{(1+\frac{1}{n})^{s}-1}{n^{s}(n+1)^{s}}=\frac{\frac{s}{n}+o(1/n)}{(n+1)^{s}})
qui est équivalent à
, l'équivalences des restes fera l'affaire , la majoration de An va introduire
et on aura le résultat
merci pour tous les intervenant je vous suis reconnaissant
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 23 Nov 2015, 02:13
juste une petite question , pour un intervalle I de R
si pour tout t dans R
)
est equivalent à
)
et si
converge uniformément , a-t-on
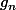
converge uniformément ?
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
par Matt_01 » 23 Nov 2015, 13:44
Il faut que ce soit "uniformément équivalent" selon moi pour conclure l'uniforme convergence de g_n, et aussi que la limite soit la fonction nulle (sinon fn(t) est équivalente à f(t) et j'ai pas l'impression que ca marcherait, mais à voir).
Par "uniforme convergence" j'entends que pour tout eps>0, il existe un n tel que pour m>n, pour tout t, |fm(t)-gm(t)|1).
Ensuite tu dois pouvoir justifier que
}{(n+1)^{s+1}}))
est inférieur à
)
à partir d'un certain rang et conclure.
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
par ilikoko123 » 23 Nov 2015, 21:11
Matt_01 a écrit:Ensuite tu dois pouvoir justifier que
est inférieur à
à partir d'un certain rang et conclure.
je sais que tu voudrais dire cela :tu dois pouvoir justifier que
}{(n+1)^{s}}))
est inférieur à
à partir d'un certain rang et conclure
c'est la clé de tout vous avez raison :we: le o(1/n) est inférieur à 1/n à partir d'un certain rang et c'est réglé , parfait merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
