Série entière

[Dyo]

Bonjour,

J'ai du mal avec cet exo, y'a un truc qui a du m'échapper.

Soit .
1) Montrer que converge uniformément sur tout compact de .
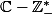
2) Développer en série au voisinage de .

Pour la 1) j'ai essayé plein de choses en vain (Weierstrass ...).
Pour la 2) j'ai essayé de calculé le coefficient mais je n'aboutis pas.

Merci pour vos indications !

[ThSQ]

z = a+ib



est une série alternée réelle donc est unif conv sur tout intervalle fermé réel sans nombre entier < 0 (le reste est majoré par le 1er terme négligée) et le truc à plumes est en sur un compact comme dit donc normalement conv.

Pour le deuze, 1/(z+n) = 1/n (1/(1+z/n))

[Dyo]

Ok merci bien ThSQ ;)

En fait ca ne fait pas vraiment référence au cours, mais plutôt à des astuces de calcul :x